5. Распределение вычислений

5.1. Параллельные циклы

5.1.1. Определение параллельного цикла

Моделью выполнения FDVM программы, как и программ на других языках с параллелизмом по данным, является модель ОПМД (одна программа - множество потоков данных). На все процессоры загружается одна и та же программа, но каждый процессор в соответствии с правилом собственных вычислений выполняет только те операторы присваивания, которые изменяют значения переменных, размещенных на данном процессоре (собственных переменных).

Таким образом, вычисления распределяются в соответствии с размещением данных (параллелизм по данным). В случае размноженной переменной оператор присваивания выполняется на всех процессорах, а в случае распределенного массива - только на процессоре (или процессорах), где размещен соответствующий элемент массива.

Определение " своих" и пропуск " чужих" операторов может вызвать значительные накладные расходы при выполнении программы. Поэтому спецификация распределения вычислений разрешается только для циклов, которые удовлетворяют следующим условиям:

• цикл является тесно-гнездовым циклом с прямоугольным индексным пространством;
• распределенные измерения массивов индексируются только регулярными выражениями типа a*I + b , где I - индекс цикла;
• левые части операторов присваивания одного витка цикла размещены на одном процессоре и, следовательно, виток цикла полностью выполняется на этом процессоре;
• нет зависимости по данным кроме редукционной зависимости и регулярной зависимости по распределенным измерениям;
• левая часть оператора присваивания является ссылкой на распределенный массив, редукционную переменную, приватную переменную (см. 5.1.3);
• нет операторов ввода-вывода и dvm-директив в теле цикла.

Цикл, удовлетворяющий этим условиям, будем называть параллельным циклом. Управляющая переменная последовательного цикла, охватывающего параллельный цикл или вложенного в него, может индексировать только локальные (размноженные) измерения распределенных массивов.

5.1.2. Распределение витков цикла. Директива PARALLEL

Параллельный цикл специфицируется следующей директивой:

Директива PARALLEL размещается перед заголовком цикла и распределяет витки циклов в соответствии с распределением массива или шаблона. Семантика директивы аналогична семантике директивы ALIGN, где индексное пространство выравниваемого массива заменяется индексным пространством цикла. Индексы циклов в списке do-variable-list перечисляются в том порядке, в котором размещены соответствующие операторы DO в тесно-гнездовом цикле.

Синтаксис и семантика отдельных частей директивы описаны в следующих разделах:

new-clause                       раздел 5.1.3
reduction-clause              раздел 5.1.4
shadow-renew-clause      раздел 6.2.2
shadow-compute-clause  раздел 6.2.3
across-clause                   раздел 6.2.4
remote-access-clause      раздел 6.3.1

Пример 5.1. Распределение витков цикла с регулярными вычислениями.

                 REAL A(N, M), B(N, M+1), C(N, M), D(N, M)
CDVM$  ALIGN ( I, J ) WITH B( I, J+1 ) :: A, C, D
CDVM$  DISTRIBUTE B ( BLOCK , BLOCK )
                     . . .
CDVM$  PARALLEL ( I, J ) ON B( I, J+1 )
                 DO 10 I = 1, N
                 DO 10 J = 1, M-1
                 A(I,J) = D(I,J) + C(I,J)
                 B(I,J+1) = D(I,J) - C(I,J)
10            CONTINUE

Цикл удовлетворяет всем условиям параллельного цикла. В частности, левые части операторов присваивания одного витка цикла A(I,J) и B(I,J+1) размещаются на одном процессоре через выравнивание массивов А и В.

Если левые части операторов присваивания размещены на разных процессорах (распределенный виток цикла), то цикл необходимо разделить на несколько циклов.

Пример 5.2. Разделение цикла

Цикл разделен на 2 цикла, каждый из которых удовлетворяет условию параллельного цикла.

5.1.3. Приватные переменные. Спецификация NEW

Если использование переменной локализовано в пределах одного витка цикла, то ее необходимо указать в спецификации NEW:

NEW-переменные (приватные переменные) не могут быть распределенными массивами. Значение приватной переменной не определено в начале витка цикла и не используется после витка цикла, поэтому в каждом витке цикла может использоваться свой экземпляр приватной переменной.

Пример 5.3. Спецификация приватной переменной.

CDVM$  PARALLEL ( I, J ) ON A( I, J ) , NEW ( X )
                 DO 10 I = 1, N
                 DO 10 J = 1, N
                 X = B(I,J) + C(I,J)
                A(I,J) = X
10           CONTINUE

5.1.4. Редукционные операции и переменные. Спецификация REDUCTION

Очень часто в программе встречаются циклы, в которых выполняются редукционные операции - в некоторой переменной суммируются элементы массива или вычисляется максимальное (минимальное) значение. Витки таких циклов можно распределять, если указать спецификацию REDUCTION.

Редукционными переменными не могут быть распределенные массивы. Редукционные переменные вычисляются и используются только в операторах определенного вида - редукционных операторах.

Введем следующие обозначения

В теле цикла редукционный оператор имеет один из следующих видов:

1)  rv = rv  op  er
     rv = er  op  rv

2)  rv = f( rv, er )
     rv = f( er, rv )
3)  if( rv  ol  er )   rv = er
   if( er  ol  rv )   rv = er

4)  if( rv  ol  er )  then 
       rv = er
       L( 1 ) = e1
         .  .  
       L( n ) = en
     endif

     if( er  ol  rv )  then 
       rv = er
       L( 1 ) = e1
        .  .  .
       L( n ) = en
     endif

Соответствие вида оператора, операции языка Фортран и имени редукции FDVM приведено в следующей таблице.

Операция MAXLOC (MINLOC) предполагает вычисление максимального (минимального) значения и определение его координат.

Пример 5.4. Спецификация редукции.

                  S = 0
                  Y =1.E10
                  X = -1.
                  IMIN(1) = 0
CDVM$  PARALLEL ( I ) ON A( I ) ,
CDVM$  REDUCTION(SUM(S), MAX(X), MINLOC(Y,IMIN,1))
                 DO 10 I = 1, N
                       S = S + A(I)
                       X = MAX(X, A(I))
                       IF(A(I) .LT. Y) THEN
                                   Y = A(I)
                                   IMIN(1) = I
                       ENDIF
10            CONTINUE

5.2. Вычисления вне параллельного цикла

Вычисления вне параллельного цикла выполняются по правилу собственных вычислений. Пусть оператор

IF p THEN lh = rh

где p – логическое выражение,
lh – левая часть оператора присваивания (ссылка на скаляр или элемент массива),
rh – правая часть оператора присваивания (выражение),

находится вне параллельного цикла.

Тогда этот оператор будет выполняться на процессоре, где распределены данные со ссылкой lh (процессор own( lh )). Все данные в выражениях p и rh должны быть размещены на процессоре own( lh ). Если какие-либо данные из выражений p и rh отсутствуют на процессоре own( lh ), то их необходимо указать в директиве удаленного доступа (см. 6.1.2) перед этим оператором.

Если lh является ссылкой на распределенный массив А и существует зависимость по данным между rh и lh, то распределенный массив необходимо размножить с помощью директивы

REDISTRIBUTE А( *,...,* ) или REALIGN А( *,...,* )

перед выполнением оператора.

Пример 5.5. Оператор собственных вычислений.

                 PARAMETER (N = 100)
                 REAL A(N, N+1), X(N)
CDVM$  ALIGN X( I ) WITH A( I, N+1)
CDVM$  DISTRIBUTE ( BLOCK, * ) :: A
                    . . .
C              обратная подстановка алгоритма Гаусса
C              собственные вычисления вне циклов
С
С              оператор собственных вычислений
С              левая и правая части – на одном процессоре
                 X(N) = A(N,N+1) / A(N,N)
                 DO 10 J = N-1, 1, -1
CDVM$  PARALLEL ( I ) ON A ( I, *)
                 DO 20 I = 1, J
                       A(I,N+1) = A(I,N+1) - A(I,J+1) * X(J+1)
20            CONTINUE
C              собственные вычисления в последовательном цикле,
С              охватывающем параллельный цикл
                 X(J) = A(J,N+1) / A(J,J)
10            CONTINUE

Отметим, что A(J,N+1) и A(J,J) локализованы на том процессоре, где размещается X(J).

6. Cпецификация удаленных данных

6.1. Определение удаленных ссылок

Удаленными данными будем называть данные, размещенные на одном процессоре и используемые на другом процессоре. Фактически эти данные являются общими (разделяемыми) данными для этих процессоров. Ссылки на такие данные будем называть удаленными ссылками. Рассмотрим обобщенный оператор

IF (…A(inda)…) B(indb) = …C(indc)…

где A, B, C - распределенные массивы,
inda, indb, indc - индексные выражения.

В модели DVM этот оператор будет выполняться на процессоре own(B(indb)), т.е. на том процессоре, где размещен элемент B(indb). Ссылка A(inda) и C(indc) не являются удаленными ссылками, если соответствующие им элементы массивов A и C размещены на процессоре own(B(indb)). Единственной гарантией этого является выравнивание A(inda), B(indb) и C(indc) в одну точку шаблона выравнивания. Если выравнивание невозможно или невыполнено, то ссылки A(inda) и/или C(indc) необходимо специфицировать как удаленные ссылки. В случае многомерных массивов данное правило применяется к каждому распределенному измерению.

По степени эффективности обработки удаленные ссылки разделены на два типа: SHADOW и REMOTE.

Если массивы B и C выровнены и

inda = indc ± d ( d – положительная целочисленная константа),

то удаленная ссылка C(indc) принадлежит типу SHADOW. Удаленная ссылка на многомерный массив принадлежит типу SHADOW, если распределяемые измерения удовлетворяют определению типа SHADOW.

Удаленные ссылки, не принадлежащие типу SHADOW, составляют множество ссылок типа REMOTE.

Особым множеством удаленных ссылок являются ссылки на редукционные переменные (см. 5.2.4), которые принадлежат типу REDUCTION. Эти ссылки могут использоваться только в параллельном цикле.

Для всех типов удаленных ссылок возможны два вида спецификаций: синхронная и асинхронная.

Синхронная спецификация задает групповую обработку всех удаленных ссылок для данного оператора или цикла. На время этой обработки, требующей межпроцессорных обменов, выполнение данного оператора или цикла приостанавливается. Асинхронная спецификация позволяет совместить вычисления с межпроцессорными обменами. Она объединяет удаленные ссылки нескольких операторов и циклов. Для запуска операции обработки ссылок и ожидания ее завершения служат специальные директивы. Между этими директивами могут выполняться другие вычисления, в которых отсутствуют ссылки на специфицированные переменные.

6.2. Удаленные ссылки типа SHADOW

6.2.1. Спецификация массива с теневыми гранями

Удаленная ссылка типа SHADOW означает, что обработка удаленных данных будет происходить через “теневые” грани. Теневая грань представляет собой буфер, который является непрерывным продолжением локальной секции массива в памяти процессора (см. рис.6.1.).Рассмотрим оператор

A( i ) = B( i + d2) + B( i – d1)

где d1, d2 – целые положительные константы. Если обе ссылки на массив B являются удаленными ссылками типа SHADOW, то массив B необходимо специфицировать в директиве SHADOW как B( d1 : d2 ), где d1 – ширина левой грани, а d2 – ширина правой грани. Для многомерных массивов необходимо специфицировать грани по каждому измерению. При спецификации теневых граней указывается максимальная ширина по всем удаленным ссылкам типа SHADOW.

Синтаксис директивы SHADOW.

Ограничение: Размер левой теневой грани (low-width) и размер правой теневой грани (high-width) должны быть целыми константными выражениями, значения которых больше или равны 0.

Задание размера теневых граней как width эквивалентно заданию width : width.

По умолчанию, распределенный массив имеет теневые грани шириной 1 с обеих сторон каждого распределенного измерения.

6.2.2. Синхронная спецификация независимых ссылок типа SHADOW для одного цикла

Синхронная спецификация является частью директивы PARALLEL:

Ограничения:

• Размер теневых граней, заполняемых значениями, не должен превышать максимального размера, описанного в директиве SHADOW.
• Если размеры теневых граней не указаны, то используются максимальные размеры.

Выполнение синхронной спецификации заключается в обновлении теневых граней значениями удаленных переменных перед выполнением цикла.

Пример 6.1. Спецификация SHADOW-ссылок без угловых элементов.

                  REAL A(100), B(100)
CDVM$   ALIGN B( I ) WITH A( I )
CDVM$   DISTRIBUTE ( BLOCK) :: A
CDVM$   SHADOW B( 1:2 )
                      . . .
CDVM$  PARALLEL ( I ) ON A ( I ), SHADOW_RENEW ( B )
                 DO 10 I = 2, 98
                        A(I) = (B(I-1) + B(I+1) + B(I+2) ) / 3
10            CONTINUE

При обновлении значений в теневых гранях используются максимальные размеры 1:2 , заданные в директиве SHADOW.

Распределение и схема обновления теневых граней показана на рис.6.1.

Рис.6.1. Распределение массива с теневыми гранями.

На каждом процессоре распределяются два буфера, которые являются непрерывным продолжением локальной секции массива. Левая теневая грань имеет размер в 1 элемент (для B(I-1)), правая теневая грань имеет размер в 2 элемента (для B(I+1) и B(I+2)). Если перед выполнением цикла произвести обмен между процессорами по схеме на рис.6.1., то цикл может выполняться на каждом процессоре без замены ссылок на массивы ссылками на буфер.

Для многомерных распределенных массивов теневые грани могут распределяться по каждому измерению. Особая ситуация возникает, когда необходимо обновлять " угол" теневых граней. В этом случае требуется указать дополнительный параметр CORNER.

Пример 6.2. Спецификация SHADOW-ссылок с угловыми элементам.

                  REAL A(100,100), B(100,100)
CDVM$  ALIGN B( I, J ) WITH A( I, J )
CDVM$  DISTRIBUTE A ( BLOCK,BLOCK)
                    . . . 
CDVM$  PARALLEL ( I, J ) ON A ( I, J ), SHADOW_RENEW ( B (CORNER))
                 DO 10 I = 2, 99
                 DO 10 J = 2, 99
                 A(I,J) = (B(I,J+1) + B(I+1,J) + B(I+1,J+1) ) / 3
10            CONTINUE

Теневые грани для массива В распределяются по умолчанию размером в 1 элемент по каждому измерению. Т.к. имеется удаленная " угловая" ссылка B(I+1,J+1) , то указывается параметр CORNER.

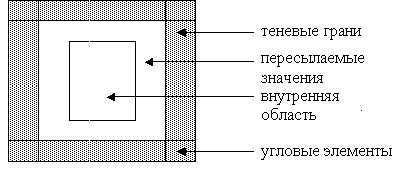
Рис. 6.2. Схема локальной секции массива с теневыми гранями.

6.2.3. Вычисление значений в теневых гранях. Спецификация SHADOW_COMPUTE

В разделах 6.2.1 и 6.2.2. были описаны способы обновления значений в теневых гранях путем обмена данными между процессорами. При этом новые значения массива вычислялись в одном цикле, а обновление производилось либо перед выполнением, либо во время выполнения другого цикла.

При некоторых условиях значения в теневых гранях можно обновлять без обмена данными между процессорами. Новые значения в теневых гранях можно вычислять в том же цикле, в котором вычисляются новые значения массивов. Такой способ обновления значений в теневых гранях описывается спецификацией SHADOW_COMPUTE, которая является частью директивы PARALLEL.

Рассмотрим некоторый параллельный цикл

CDVM$ PARALLEL (I₁ , I₂, …, I_n) ON A(f₁,f₂ ,…,f_k)

где A – идентификатор массива, в соответствии с которым распределяются витки цикла.

Пусть
{LH} - множество ссылок на распределенные массивы в левых частях операторов присваивания цикла;
{RH} - множество ссылок на распределенные массивы в правых частях (выражениях) операторов присваивания цикла.

Для применения спецификации SHADOW_COMPUTE необходимо выполнение следующих условий:

1. ширина теневых граней распределенных измерений массивов из множеств {LH} и {RH} должна быть не меньше ширины теневых граней соответствующих измерений массива A;
2. теневые грани массивов из множества {RH} должны содержать значения, соответствующие значениям массивов.

Во время выполнения цикла значения в теневых гранях массивов из множества {LH} обновляются. Ширина обновленной части каждой теневой грани равна ширине соответствующей теневой грани массива A.

Пример 6.3. Спецификация SHADOW_COMPUTE.

CDVM$   DISTRIBUTE (BLOCK) :: A, B, C, D
CDVM$   SHADOW A(1:2)
CDVM$   SHADOW B(2:2)
CDVM$   PARALLEL ( I ) ON C( I ), SHADOW_COMPUTE,
CDVM$* SHADOW_RENEW( A, B )
                  DO 10 I = 1, N
                       C( I ) = A( I ) + B( I )
                       D( I ) = A( I ) - B( I )
10             CONTINUE

Так как по умолчанию ширина теневых граней для массивов C и D равна 1, то условие 1) удовлетворяется. Выполнение спецификации SHADOW_RENEW удовлетворяет условие 2).

6.2.4. Спецификация ACROSS зависимых ссылок типа SHADOW для одного цикла

Рассмотрим следующий цикл

         DO 10 I = 2, N-1
           DO 10 J = 2, N-1
                A(I,J) = (A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J)) / 4
10      CONTINUE

Между витками цикла с индексами i1 и i2 ( i1<i2 ) существует зависимость по данным (информационная связь) массива A, если оба эти витка осуществляют обращение к одному элементу массива по схеме запись-чтение или чтение-запись.

Если виток i1 записывает значение, а виток i2 читает это значение, то между этими витками существует потоковая зависимость или просто зависимость i1®  i2.

Если виток i1 читает “старое” значение, а виток i2 записывает “новое” значение, то между этими витками существует обратная зависимость i1¬  i2.

В обоих случаях виток i2 может выполняться только после витка i1.

Значение i2 - i1 называется диапазоном или длиной зависимости. Если для любого витка i существует зависимый виток i + d (d - константа), тогда зависимость называется регулярной или зависимостью с постоянной длиной.

Цикл с регулярными вычислениями, в котором существуют регулярные зависимости по распределенным массивам, можно распределять с помощью директивы PARALLEL, указывая спецификацию ACROSS.

В спецификации ACROSS перечисляются все распределенные массивы, по которым существует регулярная зависимость по данным. Для каждого измерения массива указывается длина прямой зависимости (flow-dep-length) и длина обратной зависимости (anti-dep-length). Нулевое значение длины зависимости означает отсутствие зависимости по данным.

Ограничение:

• В каждой ссылке на массив может существовать зависимость по данным только по одному распределенному измерению. Например, разрешены ссылки A(I-1,J), A(I,J+1), но запрещены ссылки A(I-1,J+1), A(I+1,J-1).

Если в цикле обновляются не все значения массива, а только значения некоторых секций массива, то эти секции следует указать в разделе SECTION.

Пример 6.4. Спецификация цикла с регулярной зависимостью по данным.

CDVM$  PARALLEL ( I, J ) ON A( I, J ) , ACROSS ( A( 1:1, 1:1 ))
                 DO 10 I = 2, N-1
                 DO 10 J = 2, N-1
                      A(I,J) = (A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J)) / 4
10            CONTINUE

По каждому измерению массива А существует прямая и обратная зависимость длиной 1.

Спецификация ACROSS реализуется через теневые грани. Длина обратной зависимости определяет ширину обновления правой грани, а длина прямой зависимости – ширину обновления левой грани. Обновление значений правых граней производится перед выполнением цикла (как для директивы SHADOW_RENEW). Обновление левых граней производится во время выполнения цикла по мере вычисления значений удаленных данных. Фактически, ACROSS-ссылки являются подмножеством SHADOW–ссылок, между которыми существует зависимость по данным.

Эффективность параллельного выполнения цикла ACROSS

Измерение массива, по которому существует зависимость по данным, будем называть рекуррентным измерением.

Степень эффективности параллельного выполнения цикла ACROSS зависит от количества распределенных рекуррентных измерений.

Одномерный массив. Для одномерного распределенного массива с рекуррентным измерением возможно только последовательное выполнение (см. рис. 6.3).

Многомерный массив. Для многомерного массива выделим следующие сочетания рекуррентных распределенных измерений по степени убывания эффективности.

1) существует хотя бы одно не рекуррентное измерение. Массив и цикл распределяются только по этому измерению. Цикл выполняется как обычный параллельный цикл без спецификации ACROSS.

Пример 6.5. Распараллеливание по не рекуррентному измерению.

CDVM$  DISTRIBUTE A( BLOCK, * )
CDVM$  PARALLEL ( I ) ON A( I, * )
                 DO 30 I = 1,N1
                 DO 30 J = 2,N2-1
30                  A(I,J) = A(I,J-1) + A(I,J+1)

Отметим, что этот способ может быть не самым эффективным, если N1 значительно меньше N2 и количества процессоров (недостаточный параллелизм)

2) Распределено только одно рекуррентное измерение. Остальные измерения локализованы на каждом процессоре. Система поддержки организует конвейерное распараллеливание (см. рис.6.4). При этом размер ступени конвейера автоматически определяется на каждой ЭВМ, в зависимости от времени выполнения цикла и времени передачи данных при обновлении теневых граней.

Пример 6.6. Конвейерное распараллеливание.

CDVM$  DISTRIBUTE A( BLOCK, * )
CDVM$  PARALLEL ( I, J ) ON A( I, J ) ,ACROSS ( A( 1:1, 1:1 ))
                 DO 40 I = 2,N1-1
                 DO 40 J = 2,N2-1
40                  A(I,J) = A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J)

Ограничение конвейерного параллелизма. Для организации конвейерного распараллеливания необходимо выполнение дополнительных условий:

• Директива PARALLEL специфицирует как минимум два заголовка цикла. Один цикл специфицирует распределенное рекуррентное измерение, другой цикл специфицирует локальное измерение массива.
• Если в цикле ACROSS специфицируется несколько массивов, то эти массивы должны быть выровнены по рекуррентному распределенному измерению и по локальному измерению, индексируемому параллельным циклом.

3) Существует m>1 распределенных рекуррентных измерений. Массив виртуальных процессоров содержит также m измерений. Система поддержки автоматически организует параллельное выполнение по гиперплоскостям массива процессоров. Каждая гиперплоскость имеет m-1 измерение.

Пример 6.7. Распараллеливание по гиперплоскостям.

CDVM$  DISTRIBUTE A( BLOCK, BLOCK )
CDVM$  PARALLEL ( I, J ) ON A( I, J ) , ACROSS ( A( 1:1, 1:1 ))
                 DO 50 I = 2,N1-1
                 DO 50 J = 2,N2-1
50            A(I,J) = A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J)

На рис.6.5. изображен двумерный массив виртуальных процессоров. Параллельно будут выполняться вычисления на процессорах, принадлежащих одной гиперплоскости (диагональной линии).

Рис.6.3. Последовательное выполнение

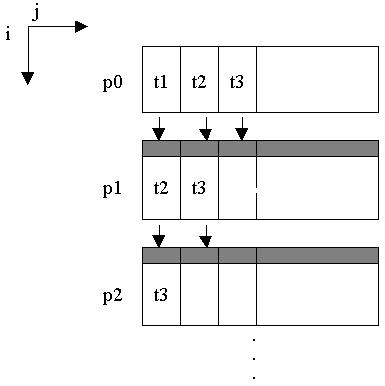
Рис.6.4. Конвейерное выполнение

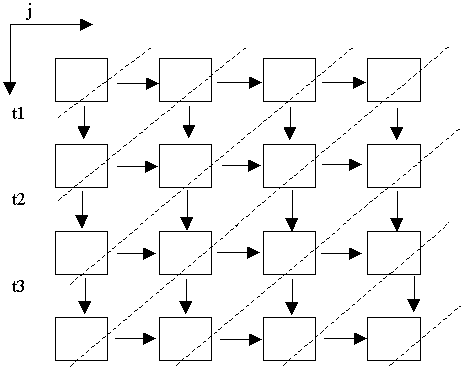
Рис.6.5. Распараллеливание по гиперплоскостям решетки виртуальных процессоров.

6.2.5. Асинхронная cпецификация независимых ссылок типа SHADOW

Обновление значений в теневых гранях, описанное в разделе 6.2.2, является неделимой (синхронной) операцией обмена для неименованной группы распределенных массивов. Эту операцию можно разделить на две операции:

• запуск обмена,
• ожидание значений.

На фоне ожидания значений теневых граней можно выполнять вычисления, в частности, вычисления на внутренней области локальной секции массива.

Асинхронное обновление теневых граней для именованной группы распределенных массивов описывается следующими директивами.

Определение группы.

Запуск обновления теневых граней.

Ожидание значений теневых граней.

Директива SHADOW_START должна выполняться после директивы SHADOW_GROUP. После выполнения директивы SHADOW_GROUP директивы SHADOW_START и SHADOW_WAIT могут выполняться многократно. Новые значения в теневых гранях могут использоваться только после выполнения директивы SHADOW_WAIT.

Особым вариантом является использование директив SHADOW_START и SHADOW_WAIT в спецификации shadow-renew-clause параллельного цикла.

Синтаксис спецификации shadow-renew-clause расширен следующим образом:

Если в спецификации указана директива SHADOW_START, то на каждом процессоре производится опережающее вычисление значений, пересылаемых в теневые грани других процессоров. После этого производится обновление теневых граней и вычисление на внутренней области локальной секции массива (см. рис.6.2).

Если в спецификации указана директива SHADOW_WAIT, то производится опережающее вычисление значений во внутренней области локальной секции массива. После завершения ожидания новых значений своих теневых граней выполняются вычисления, использующие эти значения.

Пример 6.8. Совмещение счета и обновления теневых граней.

                 REAL A(100,100), B(100,100), C(100,100), D(100,100)
CDVM$  ALIGN ( I, J ) WITH C( I, J ) :: A, B, D
CDVM$  DISTRIBUTE ( BLOCK, BLOCK ) :: C
                    . . .
CDVM$  SHADOW_GROUP AB ( A, B )
                     . . .
CDVM$  SHADOW_START AB
                    . . .
CDVM$  PARALLEL ( I, J ) ON C ( I, J ), SHADOW_WAIT AB
                 DO 10 I = 2, 99
                 DO 10 J = 2, 99
                      C(I,J) = (A(I-1,J) + A(I+1,J) + A(I,J-1) + A(I,J+1) ) / 4
                      D(I,J) = (B(I-1,J) + B(I+1,J) + B(I,J-1) + B(I,J+1) ) / 4
10            CONTINUE

Распределенные массивы по умолчанию имеют теневые грани в 1 элемент по каждому измерению. Т.к. в спецификации параллельного цикла указана директива SHADOW_WAIT, то изменяется порядок выполнения витков цикла. Сначала будут выполняться вычисления на внутренней области каждой локальной секции массива, затем выполнится директива ожидания новых значений теневых граней. Выполнение цикла завершается вычислением значений пересылаемых в теневые грани.

6.3. Удаленные ссылки типа REMOTE

6.3.1. Директива REMOTE_ACCESS

Удаленные ссылки типа REMOTE специфицируются директивой REMOTE_ACCESS.

Директива REMOTE_ACCESS может быть отдельной директивой (область действия - следующий оператор) или дополнительной спецификацией в директиве PARALLEL (область действия – тело параллельного цикла).

Если удаленная ссылка задается как имя массива без списка индексов, то все ссылки на этот массив в параллельном цикле (операторе) являются удаленными ссылками типа REMOTE.

Рассмотрим удаленную ссылку на многомерный распределенный массив

A( ind₁, ind₂,…,ind_k )

Пусть ind_j – индексное выражение по j-ому измерению.

В директиве REMOTE_ACCESS индексное выражение указывается без изменений, если

• j-ое измерение является распределенным измерением,
• ind_j = a * i + b, где a и b не изменяются в процессе выполнения цикла (инварианты).

Во всех остальных случаях в директиве REMOTE_ACCESS вместо ind_j указывается “:” (все измерение).

6.3.2. Синхронная спецификация удаленных ссылок типа REMOTE

Если в директиве REMOTE_ACCESS не указано имя группы (remote-group-name), то выполнение такой директивы происходит в синхронном режиме. В пределах нижестоящего оператора или параллельного цикла компилятор заменяет все вхождения удаленной ссылки ссылкой на буфер. Пересылка удаленных данных производится перед выполнением оператора или цикла.

Пример 6.9. Синхронная спецификация удаленных ссылок типа REMOTE.

                 DIMENSION A(100,100), B(100,100)
CDVM$  DISTRIBUTE (*,BLOCK) :: A
CDVM$  ALIGN B( I, J ) WITH A( I, J )
                     . . .
CDVM$  REMOTE_ACCESS ( A(50,50) )
С               замена ссылки A(50,50) ссылкой на буфер
С               рассылка значения A(50,50) по всем процессорам
1               X = A(50,50)
                    . . .
CDVM$  REMOTE_ACCESS ( B(100,100) )
С               пересылка значения В(100,100) в буфер процессора own(A(1,1)
2               A(1,1) = B(100,100)
                     . . .
CDVM$  PARALLEL (I,J) ON A(I,J) , REMOTE_ACCESS ( B(:,N) )
С               рассылка значений B(:,N) по процессорам own(A(:,J))
3               DO 10 I = 1, 100DO 10 J = 1, 100
10             A(I,J) = B(I,J) + B(I,N)

Первые две директивы REMOTE_ACCESS специфицируют ервые две директивы удаленные ссылки для отдельных операторов. цикле специфицирует REMOTE_ACCESS в параллельном удаленные данные которые распределен матрицы) для всех процессоров, на (столбец массив А.

6.3.3. Асинхронная спецификация удаленных ссылок типа REMOTE

Если в директиве REMOTE_ACCESS указано имя группы (remote-group-name), то выполнение директивы происходит в асинхронном режиме. Для спецификации этого режима необходимы следующие дополнительные директивы.

Описание имени группы.

Идентификатор, определенный этой директивой, может использоваться только в директивах REMOTE_ACCESS , PREFETCH и RESET. Группа remote-group представляет собой глобальный объект, областью действия которого является вся программа.

Рассмотрим следующую типовую последовательность асинхронной спецификации удаленных ссылок типа REMOTE.

CDVM$  REMOTE_GROUP RS
10                 . . .
CDVM$  PREFETCH RS
                     . . .
C              вычисления, в которых не участвуют удаленные ссылки r₁ , …,r_n
                   . . .
CDVM$  PARALLEL . . . , REMOTE_ACCESS (RS : r₁)
                      . . .
CDVM$  REMOTE_ACCESS (RS : r_i)
                     . . .
CDVM$  PARALLEL . . . , REMOTE_ACCESS (RS : r_n)
                    . . .
                 IF( P ) GO TO 10

При первом прохождении указанной последовательности операторов директива PREFETCH не выполняется. Директивы REMOTE_ACCESS выполняется в обычном синхронном режиме. При этом происходит накопление ссылок в переменной RS. После выполнения всей последовательности директив REMOTE_ACCESS значение переменной RS равно объединению подгрупп удаленных ссылок r_i E ...E r_n.

При втором и последующих прохождениях директива PREFETCH осуществляет упреждающую пересылку удаленных данных для всех ссылок, составляющих значение переменной RS. После директивы PREFETCH и до первой директивы REMOTE_ACCESS с тем же именем группы можно выполнять другие вычисления, которые перекрывают ожидание обработки удаленных ссылок. При этом директивы REMOTE_ACCESS никакой пересылки данных уже не вызывают.

Ограничения.

• Повторное выполнение директивы PREFETCH является корректным только в том случае, когда характеристики группы удаленных ссылок (параметры циклов, распределения массивов и значения индексных выражений в удаленных ссылках) не меняются.
• Директиву PREFETCH можно выполнять для нескольких циклов (нескольких директив REMOTE_ACCESS), если между этими циклами не существует зависимости по данным для распределенных массивов, указанных в директивах REMOTE_ACCESS .

Если характеристики группы удаленных ссылок изменились, то необходимо присвоить неопределенное значение группе удаленных ссылок с помощью директивы RESET, после чего будет происходить новое накопление группы удаленных ссылок.

Рассмотрим следующий фрагмент многообластной задачи. Область моделирования разделена на 3 подобласти, как показано на рис.6.6.

Рис.6.6. Разделение области моделирования.

Пример 6.10. Использование группы регулярных удаленных ссылок.

                 REAL A1(M,N1+1), A2(M1+1,N2+1), A3(M2+1,N2+1)
CDVM$  DISTRIBUTE ( BLOCK,BLOCK) :: A1, A2, A3
CDVM$  REMOTE_GROUP RS
                 DO 1 ITER = 1, MIT
                     . . .
C              обмен границами по линии раздела D
CDVM$  PREFETCH RS
                     . . .
CDVM$  PARALLEL ( I ) ON A1 ( I, N1+1 ), REMOTE_ACCESS ( RS: A2(I,2))
                 DO 10 I = 1, M1
10                  A1(I,N1+1) = A2(I,2)
CDVM$  PARALLEL ( I ) ON A1 ( I, N1+1 ), REMOTE_ACCESS ( RS: A3(I-M1,2))
                 DO 20 I = M1+1, M
20                  A1(I,N1+1) = A3(I-M1,2)
CDVM$  PARALLEL ( I ) ON A2 ( I, 1 ), REMOTE_ACCESS ( RS: A1(I,N1))
                 DO 30 I = 1, M1
30                  A2(I,1) = A1(I,N1)
CDVM$  PARALLEL ( I ) ON A3 ( I, 1 ), REMOTE_ACCESS ( RS: A1(I+M1,N1))
                 DO 40 I = 1, M2
40                  A3(I,1) = A1(I+M1,N1)
                    . . .
                 IF (NOBLN) THEN
C              перераспределение массивов с целью балансировки загрузки
                    . . .
CDVM$  RESET RS
                 END IF
                     . . .
1              CONTINUE

6.3.4. Асинхронное копирование по ссылкам типа REMOTE

Если в параллельном цикле содержатся только операторы присваивания без вычислений, то доступ по ссылкам типа REMOTE можно выполнять более эффективно с помощью асинхронного копирования распределенных массивов.

6.3.4.1. Цикл и операторы копирования

Рассмотрим следующий цикл

DO 10 I₁ = L₁,H₁,S₁
      .  .  .
DO 10 I_n = L_n,H_n,S_n
10 A(f₁,…,f_k) = B (g₁,…,g_m)

где    A, B - идентификаторы разных распределенных массивов.

L_i,H_i,S_i – инварианты цикла
f_i = a_i *I_i + b_i
g_j = c_j *I_j + d_j
a_i, b_i , c_j, d_j – целые выражения, инварианты цикла (выражения, значения которых не изменяются в процессе выполнения цикла).

Каждая переменная цикла I_l может быть использована не более чем в одном выражении f_i и не более чем в одном выражении g_j.

Цикл может содержать несколько операторов, удовлетворяющих вышеуказанным ограничениям. Такой цикл будем называть циклом копирования (copy-loop).

Цикл копирования может быть описан одним или несколькими операторами копирования (copy-statement) следующего вида

A(a ₁,…,a _k) = B(b ₁,…,b _m)

где
a _i = l_i : h_i : s_i
b _j = l_j : h_j : s_j
a _i, b _j - являются триплетами языка Фортран 90.

Оператор копирования является аналогом оператора присваивания секций массивов Фортран 90.

Для триплетов существуют правила сокращенной записи. Определим эти правила на примере триплета a _i.

1. Если в копировании участвует все измерение массива, то
   a _i =  :
2. Если s_i = 1, то
   a _i = l_i : h_i
3. Если L_i = h_i , то

4. a _i = l_i

Для цикла копирования 10 выражения триплетов определяются следующим образом

Рассмотрим следующий цикл копирования

            REAL A(N1,N2,N3), B(N1,N3)
            DO 10 I1 = 1, N1
            DO 10 I2 = 2, N3-1
10       A(I1, 5, I2+1) = B(I1, I2-1)

Этому циклу соответствует следующий оператор копирования

A( :, 5, 3:N3 ) = B( :, 1:N3-2 )

6.3.4.2. Директивы асинхронного копирования

Асинхронное копирование позволяет совместить передачу данных между процессорами с выполнением других операторов.

Асинхронное копирование определяется комбинацией директивы начала копирования (ASYNCHRONOUS  ID) и директивой ожидания окончания копирования (ASYNCWAIT  ID). Соответствие директив определяется одним идентификатором ID.

6.3.4.2.1. Директива ASYNCID

Директива ASYNCID описывает отдельный идентификатор для каждой пары директив асинхронного копирования.

Синтаксис директивы:

6.3.4.2.2. Директива F90

Директива F90 является префиксом для каждого оператора копирования.

Синтаксис.

6.3.4.2.3. Директивы ASYNCHRONOUS и END ASYNCHRONOUS

Директивы ASYNCHRONOUS и END ASYNCHRONOUS задают блочную конструкцию.

Синтаксис.

Все операторы присваивания в циклах копирования (copy-loop) должны быть описаны директивами F90 с соответствующим оператором копирования.

6.3.4.2.4. Директива ASYNCWAIT

Синтаксис.

Пример из раздела 6.3.4.1 можно специфицировать как асинхронное копирование следующим образом.

CDVM$  ASYNCID TR
                 REAL A(N1,N2,N3), B(N1,N3)
       . . .
CDVM$  ASYNCHRONOUS TR
CDVM$  F90 A( :, 5, 3:N3 ) = B( :, 1:N3-2 )
                 DO 10 I1 = 1, N1
                 DO 10 I2 = 2, N3-1
10            A(I1, 5, I2+1) = B(I1, I2-1)
CDVM$  END ASYNCHRONOUS
                 . . .
                 последовательность операторов,
                 которая выполняется на фоне передачи данных
               . . .
CDVM$  ASYNCWAIT TR

6.4. Удаленные ссылки типа REDUCTION

6.4.1. Синхронная спецификация удаленных ссылок типа REDUCTION

Если спецификация REDUCTION в параллельном цикле указана без имени группы, то она является синхронной спецификацией и выполняется следующим образом.

1. Вычисление локальной редукции. В процессе выполнения цикла на каждом процессоре вычисляется локальное значение редукции для той части данных, которые распределены на процессоре.
2. Вычисление глобальной редукции. После окончания выполнения цикла автоматически вычисляется межпроцессорная редукция локальных значений. Полученное значение присваивается редукционной переменной на каждом процессоре.

6.4.2. Асинхронная спецификация удаленных ссылок типа REDUCTION

Асинхронная спецификация позволяет:

• объединять в одну группу редукционные переменные, вычисляемые в разных циклах;
• совмещать выполнение глобальной групповой редукции с другими вычислениями.

Для асинхронной спецификации, кроме директивы REDUCTION (с именем группы), необходимы следующие дополнительные директивы.

Типовая последовательность директив асинхронной спецификации типа REDUCTION выглядит следующим образом.

CDVM$  REDUCTION_GROUP RD
                     . . .
CDVM$  PARALLEL ... , REDUCTION (RD : d₁)
C               локальная редукция d₁
                    . . .
CDVM$  PARALLEL ... , REDUCTION (RD : d_n)
C              локальная редукция d_n
                    . . .
CDVM$  REDUCTION_START RD
C              начало глобальной редукции d_iU...U d_n
                   . . .
CDVM$  REDUCTION_WAIT RD
C              конец глобальной редукции d_i U ... U d_n

Ограничения.

• До выполнения директивы REDUCTION_START включенные в группу редукционные переменные могут использоваться только в редукционных операторах параллельных циклов.
• Директива REDUCTION_START и REDUCTION_WAIT должны выполняться после окончания цикла (циклов), где вычислялись локальные значения редукционных переменных. Между этими операторами могут выполняться только те операторы, в которых не используются значения редукционных переменных.
• Директива REDUCTION_WAIT уничтожает группу редукционных операций.

Пример 6.11. Асинхронная спецификация типа REDUCTION..

CDVM$   DISTRIBUTE A ( BLOCK )
CDVM$   ALIGN B( I ) WITH A( I )
CDVM$   REDUCTION_GROUP RD
                       . . .
                   S = 0
CDVM$   PARALLEL ( I ) ON A( I ),
CDVM$* REDUCTION ( RD : SUM(S))
                  DO 10 I = 1, N
10              S = S + A(I)
                  X = 0.
CDVM$   PARALLEL ( I ) ON B( I ),
CDVM$* REDUCTION ( RD : MAX(X))
                  DO 20 I = 1, N
20              X = MAX(X, ABS( B(I) ) )
CDVM$   REDUCTION_START RD
C               начало глобальной редукции SUM(S) и MAX(X)
CDVM$   PARALLEL ( I ) ON A( I )
                  DO 30 I = 1, N
30             A(I) = A(I) + B(I)
CDVM$  REDUCTION_WAIT RD
C               конец глобальной редукции
                  PRINT *, S, X

На фоне выполнения групповой редукции будут вычисляться значения элементов массива А.