
| C-DVM - contents | Part 1(1-4) | Part 2 (5-11) | Part 3 (Appendixes) |
| created: april, 2001 | - last edited 08.10.02 - |
5 Distribution of computations
5.1.1 Parallel loop definition
The execution model of C-DVM program as the programs in other languages with data parallelism is SPMD (single program, multiple data). All the processors are loaded by the same program, but each processor performs only those assignment statements that modify values of the variables located on this processor (own variables) according to the rule of own computations.
Thus the computations are distributed in accordance with data mapping (data parallelism). In the case of a replicated variable, the assignment statement is performed at all the processors. In the case of a distributed array, the assignment statement is performed only at the processor (or the processors) where corresponding array element is located.
Identification of "own" statements and missing "others" can cause essential overhead during the program execution. Therefore a specification of distributed computations is permitted only for loops, satisfying the following requirements.
A loop, satisfying these requirements is named parallel loop. An iteration variable of sequential loop, surrounding the parallel loop, or nested in the loop, can indexise local (replicated) dimensions of distributed arrays only.
5.1.2 Distribution of loop iterations. PARALLEL directive
A parallel loop is specified by the following directive:
| parallel-directive | ::= PARALLEL loop-variable... ON iteration-align-spec [ ; reduction-clause] [ ; shadow-renew-clause] [ ; remote-access-clause ] [ ; across-clause ] |
| iteration-align-spec | ::= align-target iteration-align-subscript-string |
| iteration-align-subscript | ::= [ int-expr ] |
| | [ do-variable-use ] | |
| | [] | |
| loop-variable | ::= [ do-variable ] |
| do-variable-use | ::= [ primary-expr
* ] do-variable [ add-op primary-expr ] |
Note. Headers of nested loop should be written with macros DO(var,first,last,step) and FOR(var,times) (shorthand for DO(var,0,times-1,1)).
PARALLEL directive is placed before loop header and distributes loop iterations in accordance with array or template distribution. The directive semantics is similar to semantics of ALIGN directive, where index space of distributed array is replaced by the loop index space. The order of loop indexes in list loop-variable... corresponds to the order of corresponding DO statements in tightly nested loop.
Syntax and semantics of the parts of the directive are described in the sections:
| reduction-clause | section 5.1.4, |
| shadow-renew-clause | section 6.2.2, |
| remote-access-clause | section 6.3.1, |
| across-clause | section 6.2.3. |
Example 5.1. Distribution of loop iterations with regular computations.
DVM(DISTRIBUTE B [BLOCK ][BLOCK]) float B[N][M+1];
DVM(ALIGN [i][j] WITH B[i][j+1]) float A[N][M], C[N][M], D[N][M];
. . .
DVM(PARALLEL [i][j] ON B[i][j+1])
DO(i, 0, N-1, 1)
DO(j, 0, M-2, 1)
{
A[i][j] = D[i][j] + C[i][j];
B[i][j+1] = D[i][j] – C[i][j];
}
The loop satisfies to all requirements of a parallel loop. In particular, left sides of assignment statements of one loop iteration A[i][j] and B[i][j+1] are allocated on one processor through alignment of arrays A and B.
If left sides of assignment operators are located on the different processors (distributed iteration of the loop) then the loop must be split on several loops.
In following example a variable is described inside loop. It is, so called, a private variable, i.e. its value is inessensial at iteration beginning and unused after the iteration. The variables described outside the loop must not be used in such manner because of two possible problems of parallel execution of the loop iterations: data dependency between iiterations and inconsistent state of the variable after leaving the loop.
Example 5.3. Declaration of private variable.
DVM(PARALLEL [i]]j] ON A[i][j] )
FOR(i, N)
FOR(j, N)
{float x; /* variable declared as private for every iteration */
x = B[i][j] + C[i][j];
A[i][j] = x;
}
5.1.4 Reduction operations and variables. REDUCTION specification
Programs often contain loops with so called reduction operations: array elements are accumulated in some variable, minimum or maximum value of them is calculated. Iterations of such loops may be distributed using REDUCTION specification.
| reduction-clause | ::= REDUCTION reduction-op... |
| reduction-op | ::= reduction-op-name ( reduction-variable ) |
| | reduction-loc-name (reduction-variable, loc-variable) |
|
| reduction-variable | ::= array-name |
| | scalar-variable-name | |
| reduction-op-name | ::= SUM |
| | PRODUCT | |
| | MAX | |
| | MIN | |
| | AND | |
| | OR | |
| reduction-loc-name | ::= MAXLOC |
| | MINLOC |
Distributed arrays cannot be used as reduction variables. Reduction variables are calculated and used only in certain statements - reduction statements.
The second argument of the MAXLOC and MINLOC operations is a variable describing the location of the element with found maximal (and correspondently minimal) value. Usually, it is an index of one-dimensional array element or a structure, containing index values of multi-dimensional array.
Example 5.4. Specification of reduction.
S = 0;
X = A[0];
Y = A[0];
MINI = 0;
DVM(PARALLEL [i] ON A[i];
REDUCTION SUM(S) MAX(X) MINLOC(Y,MIMI))
FOR(i, N)
{
S = S + A[i];
X = max(X, A[i]);
if(A[i] < Y) {
Y = A[i];
MINI = i;
}
}
5.2 Calculations outside parallel loop
The calculations outside a parallel loop is performed according to own computation rule. Asignment statement
lh = rh;
can be executed on some processor only if lh is located at this processor. If lh is an distributed array element (and is not located on all the processors), then the statement (own computation statement) will be executed only on the processor (or on the processors), where given element is allocated. All data, used in rh expresions, must be located on the processor. If some data from expressions lh and rh are not located on the processor, they must be specified in remote access directive (see section 6.1.2) prior the statement.
If lh is reference to distributed array A, and data dependence between rh and lh exists, it is necessary to replicate distributed array by REDISTRIBUTE A[]...[] or REALIGN A[]...[] directive.
Example 5.5. Own computations.
#define N 100 DVM(DISTRIBUTE [BLOCK][]) float A[N][N+1]; DVM(ALIGN [I] WITH A[I][N+1]) float X[N]; . . . /* reverse substitution of Gauss algorithm */ /* own computations outside the loops */ X[N-1] = A[N-1][N] / A[N-1][N] DO(J, N-2,0, -1) DVM(PARALLEL [I] ON A [I][]; REMOTE_ACCESS X[j+1]) DO(I,0, J,1) A[I][N] = A[I][N] – A[I][J+1] * X[J+1]; /* own computations in sequential loop, */ /* surrounding the parallel loop */ X[J] = A[J][N] / A[J][J] }
Note, that A[J][N+1] and A[J][J] are localized on the processor, where X[J] is allocated.
6.1 Remote reference definition
Data, allocated on one processor and used on the other one, are called remote data. The references to such data are called remote references. Consider generalized statement
if (…A[inda]…) B[indb] = …C[indc]…
where
A, B, C - distriduted arrays,
inda, indb, indc – index expressions.
In DVM model this statement will be performed on the processor, where element B(indb) is allocated. A(inda) and C(indc) references are not remote references, if corresponding elements of arrays A and C are allocated on the same processor. This is guarantied only if A(inda), B(indb) and C(indc) are aligned in the same point of alignment template. If alignment is impossible, then the references A(inda) and/or C(indc) should be specified as remote references. In the case of multidimensional arrays this rule is applied to every distributed dimension.
By a degree of processing efficiency remote references are subdivided on two types: SHADOW and REMOTE.
If B and C arrays are aligned and
inda = indc ± d ( d – positive integer constant),
the remote reference C(indc) is SHADOW type reference. The remote reference to multidimensional array is SHADOW type reference, if distributed dimensions satisfy to SHADOW type definition.
Remote references that are not SHADOW type references, are the references of REMOTE type.
Special set of remote references is set of references to reduction variables (see section 5.2.4), that are REDUCTION type references. These references can be used in parallel loop only.
There are two kinds of specifications: synchronous and asynchronous for all types of remote references.
Synchronous specification defines group processing of all remote references for given statement or loop. During the processing, requiring interprocessor exchanges, the statement or the loop execution is suspended.
Asynchronous specification allows overlapping computations and interprocessor exchanges. It unites remote references of several statements and loops. To start reference processing operation and wait for its completion, special directives are used. Other computations, not containing references to specified variables, can be executed between these directives.
6.2 Remote references of SHADOW type
6.2.1 Specification of array with shadow edges
Remote reference of SHADOW type means, that remote data processing will be organized using shadow edges. Shadow edge is a buffer, that is continuous prolongation of array local section in the processor memory (see fig.6.1). Consider the following statement:
A[i] = B[i + d2] + B[ i – d1]
where d1,d2 are integer positive constants. If both referencies to array B are remote references of SHADOW type, then SHADOW [ d1 : d2] clause should be used for B array, where d1 is low edge width and d2 is high edge width. For multidimensional arrays edges for all dimensions should be specified. When shadow edges are specified, maximal width for all remote referencies of SHADOW type is defined.
Syntax of SHADOW directive.
| shadow-directive | ::= SHADOW shadow-array... |
| shadow-array | ::= array-name shadow-edge... |
| shadow-edge | ::= [ width ] |
| | [ low-width : high-width ] | |
| width | ::= int-expr |
| low-width | ::= int-expr |
| high-width | ::= int-expr |
Constraint. Low shadow edge width (low-width) and high shadow edge width (high-width) must be non-negative integer constant expressions.
Specificating shadow edge width as width is equivalent to the specification width : width.
The width of the both shadow edges of a distributed array is equal to 1 for each distributed dimension by default.
6.2.2 Specification of independent references of SHADOW type for one loop
Specification of shadow edge synchronous renewing is PARALLEL directive clause:
| shadow-renew-clause | ::= SHADOW_RENEW renewee... |
| renewee | ::= dist-array-name [ shadow-edge ]… [ CORNER ] |
Constraints:
Synchronous specification execution is renewing shadow edges by values of remote variables before entering the loop.
Example 6.1. Specification of SHADOW-references without corner elements.
DVM(DISTRIBUTE [BLOCK]) float A[100]; DVM(ALIGN[I] WITH A[I]; SHADOW [1:2]) float B[100]; . . . DVM(PARALLEL[I] ON A[I]; SHADOW_RENEW B) DO(I,1, 97,1) A[I] = (B[I-1] + B[I+1] + B[I+2]) / 3.;
When renewing shadow edges the maximal widths 1:2 specified in SHADOW directive are used.
Distribution and scheme of renewing shadow edges is shown on fig. 6.1.

Fig.6.1. Distribution of array with shadow edges.
Two buffers, that are continuous prolongation of the array local section, are allocated on each processor. The low shadow edge width is equal to 1 element (for B[I-1]), high shadow edge width is equal to 2 elements (B[I+1] and B[I+2]). If before loop entering to perform processor exchange according to scheme on fig. 6.1, the loop can be executed on each processor without replacing references to the arrays by references to the buffer.
Shadow edges for multidimensional distributed arrays can be specified for each dimension. A special case is when it is required to renew "a corner" of shadow edges. In such a case additional parameter CORNER is needed.
Example 6.2. Specification of SHADOW-references with corner elements.
DVM(DISTRIBUTE [BLOCK]) float A[100]; DVM(DISTRIBUTE [BLOCK][BLOCK]) float A[100][100]; DVM(ALIGN [i][j] WITH A[i][j]) float B[100][100]; . . . DVM(PARALLEL[I][J] ON A[I][J]; SHADOW_RENEW B CORNER) DO( I, 1, 98, 1) DO( J, 1, 98, 1) A[I][J] = (B[I][J+1] + B[I+1][J] + B[I+1][J+1]) / 3.;
The widths of shadow edges of the array B are equal to 1 element for all dimensions by default. As "corner" reference B[I+1][J+1] exists, the CORNER parameter is specified.
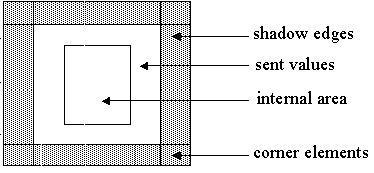
Fig 6.2. Scheme of array local section with shadow edges.
6.2.3 ACROSS specification of dependent references of SHADOW type for single loop
Consider the following loop
DO(i, 1, N-2,1) DO(j, 1, N-2,1) A[i][j] =(A[i][j-1]+A[i][j+1]+A[i-1][j]+A[i+1][j])/4.;
The dependence of A array data (informational linkage) exists between loop iterations with indexes i1 and i2 ( i1<i2), if both iterations refer to the same array element by write-read or read-write scheme.
If iteration i1 writes a value and iteration i2 reads this value, then flow dependence, or simply dependence i1® i2 exists between the iterations.
If iteration i1 reads the "old" value and iteration i2 writes the "new" value, then reverse (anti) dependence i1¬ i2 exists between the iterations.
In both cases the iteration i2 can be executed only after the iteration i1.
The value i2 - i1 is named a range or length of the dependence. If for any iteration i dependent iteration i + d (d is constant) exists, then the dependence is called regular one, or dependence with constant length.
The loop with regular computations, with regular dependencies on distributed arrays, can be distributed with PARALLEL directive, using ACROSS specification.
| across-clause | ::= ACROSS dependent-array... |
| dependent-array | ::= dist-array-name dependence... |
| dependence | ::= [ flow-dep-length : anti-dep-length ] |
| flow-dep-length | ::= int-constant |
| anti-dep-length | ::= int-constant |
All the distributed arrays with regular data dependence are specified in ACROSS specification. The length of flow-dependence (flow-dep_length) and the length of reverse (anti) dependence (anti-dep-length) are specified for each dimension of the array. There is no data dependence, if length is equal to zero.
Example 6.3. Specification of the loop with regular data dependence.
DVM(PARALLEL [i][j] ON A[i][j] ; ACROSS A[1:1][1:1]) DO(i , 1, N-2, 1) DO(j , 1, N-2, 1) A[i][j]=(A[i][j-1]+A[i][j+1]+A[i-1][j]+A[i+1][j])/4.;
Flow- and anti-dependencies of lenght 1 exist for each dimension of the array A.
ACROSS specification is implemented via shadow edges. Anti-dependence length defines width of high edge renewing, and flow-dependence length defines width of low edge renewing. High edges are renewed prior the loop execution (as for SHADOW_RENEW directive). Low edges are renewed during the loop execution as remote data calculation proceeds. It allows to organize so called wave calculations for multidimensional arrays. Actually, ACROSS-references are subset of SHADOW-references, that have data dependences.
6.2.4 Asynchronous specification of independent references of SHADOW type
Updating values of shadow edges, described in section 6.2.2, is indivisible (synchronous) exchange operation for unnamed group of distributed arrays. The operation can be divided into two operations:
While waiting for shadow edge values, other computations can be performed, in particular, the computations on internal area of the local array section can be done.
The following directives describe asynchronous renewing of shadow edges for named group of distributed arrays.
Declaration of a group.
| shadow-group-directive | ::= CREATE_SHADOW_GROUP shadow-group-name : renewee… |
Start of shadow edges renewing.
| shadow-start-directive | ::= SHADOW_START shadow-group-name |
Waiting for shadow edges values.
| shadow-wait-directive | ::= SHADOW_WAIT shadow-group-name |
SHADOW_START directive must be executed after CREATE_SHADOW_GROUP one. After CREATE_SHADOW_GROUP directive execution directives SHADOW_START and SHADOW_WAIT can be executed many times. Updated values of the shadow edges may be used only after SHADOW_WAIT directive.
A special case is using SHADOW_START and SHADOW_WAIT directives in specification shadow-renew-clause of parallel loop.
| shadow-renew-clause | ::= . . . |
| | shadow-start-directive | |
| | shadow-wait-directive |
If SHADOW_START directive is specified in a parallel loop, the surpassing computation of the values, sent to the shadow edges. Then the shadow edges are renewed and the computation on internal area of the array local section is done (see fig. 6.2).
If SHADOW_WAIT directives are specified in a parallel loop, the surpassing computation of the values not using shadow edge elements is performed. Other elements are calculated only after completion of waiting for new values of shadow edges.
Example 6.4. Overlapping computations and shadow edges updating.
DVM(DISTRIBUTE [BLOCK][BLOCK]) float C[100][100];
DVM(ALIGN[I][J] WITH C[I][J]) float A[100][100], B[100][100],
D[100][100];
DVM(SHADOW_GROUP) void *AB;
. . .
DVM(CREATE_SHADOW_GROUP AB: A B);
. . .
DVM(SHADOW_START AB);
. . .
DVM(PARALLEL[I][J] ON C[I][J]; SHADOW_WAIT AB)
DO( I , 1, 98, 1)
DO( J , 1, 98, 1)
{ C[I][J] = (A[I-1][J]+A[I+1][J]+A[I][J-1]+A[I][J+1])/4.;
D[I][J] = (B[I-1][J]+B[I+1][J]+B[I][J-1]+B[I][J+1])/4.;
}
The shadow edge width of distributed arrays A and B is equal to 1 element for each dimension by default. Waiting for completion of shadow edges renewing is postponed as late as possible, that is, up to the moment when the computations can not be continued without them.
6.3 Remote references of REMOTE type
Remote references of REMOTE type is specified by REMOTE_ACCESS directive.
| remote-access-directive | ::= REMOTE_ACCESS [ remote-group-name : ] regular-reference... |
| regular-reference | ::= dist-array-name [ regular-subscript ]… |
| regular-subscript | ::= [ int-expr ] |
| | [ do-variable-use ] | |
| | [] | |
| remote-access-clause | ::= remote-access-directive |
REMOTE_ACCESS directive can be used as a separate directive prior to own computation statement (its operating area - next statement) or as additional specification in PARALLEL directive (its operating area - parallel loop body).
If remote reference is specified as array name without index list, then all references to the array in a parallel loop (in a statement) are remote references of REMOTE type.
6.3.2 Synchronous specification of remote references of REMOTE type
If in REMOTE_ACCESS directive a group name (remote-group-name) is not specified the directive is executed in synchronous mode. In boundaries of a statement or a parallel loop below the compiler replaces all remote references by the references to a buffer. The values of remote variable are passed prior the statement or the loop execution.
Example 6.5. Synchronous specification of remote references of REMOTE type.
DVM(DISTRIBUTE [][BLOCK]) float A[100][100], B[100][100];
. . .
DVM(REMOTE_ACCESS A[50][50]) X = A[50][50];
. . .
DVM(REMOTE_ACCESS B[100][100]) {A[1][1] = B[100][100];}
. . .
DVM(PARALLEL[I][J] ON A[I][J]; REMOTE_ACCESS B[][N])
FOR(I, 100)
FOR(J, 100)
A[I][J] = B[I][J] + B[I][N];
Two first REMOTE_ACCESS directives specify remote references for own computation statements. REMOTE_ACCESS directive in parallel loop specifies remote data (matrix column) for all processors the array A is mapped on.
6.3.3 Asynchronous specification of remote references of REMOTE type
If in REMOTE_ACCESS directive a group name (remote-group-name) is specified the directive is executed in asynchronous mode. To specify this mode following additional directives are required.
Group name definition.
| remote-group-directive | ::= REMOTE_GROUP |
The identifier, defined in the directive, can be used only in REMOTE_ACCESS, PREFETCH and RESET directives.
| prefetch-directive | ::= PREFETCH group-name |
| reset-directive | ::= RESET group-name |
Consider the following typical asynchronous specification sequence of remote references of REMOTE type:
DVM(REMOTE_GROUP) void * RS; . . . DVM(PREFETCH RS); . . . DVM(PARALLEL . . . ; REMOTE_ACCESS RS : r1) . . . DVM(PARALLEL . . . ; REMOTE_ACCESS RS : rn) . . .
When given sequence of statements is executed first time, PREFETCH directive is not executed. REMOTE_ACCESS directives are executed in usual synchronous mode. At that the references are accumulated in RS variable. After execution of all sequence of REMOTE_ACCESS directives the value of RS variable is union of subgroups of remote references ri , ..., rn.
When the sequence is executed the second and next time, PREFETCH directive performs surpassed sending of remote data for all the references, contained in RS variable. After PREFETCH directive and up to first executable REMOTE_ACCESS directive other computations overlapping waiting for remote reference processing, can be performed. At that REMOTE_ACCESS directives don't send any data.
Constraints.
If remote reference group characteristics are updated it is necessary to assign to the group undefined value using RESET directive. The new accumulation of remote reference group will be performed.
Consider the following fragment of multi-block problem. Simulation area is split on 3 blocks as is shown in fig. 6.3.
Fig. 6.3. Splitting simulation area.
Example 6.6. Using named group of regular remote references.
DVM (DISTRIBUTE [BLOCK][BLOCK])
float A1[M][N1+1], A2[M1+1][[N2+1], A3[M2+1][N2+1];
DVM (REMOTE_GROUP) void *RS;
DO(ITER,1, MIT,1)
{
. . .
/* edge exchange by split line D */
DVM (PREFETCH RS);
. . .
DVM ( PARALLEL[i] ON A1[i][N1]; REMOTE_ACCESS RS: A2[i][1])
DO(i,0, M1-1,1)
A1[i][N1] = A2[i][1];
DVM (PARALLEL[i] ON A1[i][N1]; REMOTE_ACCESS RS: A3[i-M1][1])
DO(i,M1, M-1,1)
A1[i][N1] = A3[i-M1][1];
DVM (PARALLEL[i] ON A2[i][0]; REMOTE_ACCESS RS: A1[I][N1-1])
DO(i,0, M1-1,1)
A2[i][0] = A1[i][N1-1];
DVM(PARALLEL[i] ON A3[i][0]; REMOTE_ACCESS RS: A1[I+M1][N1-1])
DO (i,0, M2-1,1) A3[i][0] = A1[i+M1][N1-1];
. . .
if (NOBLN) {
/*array redistribution to balance loading */
. . .
DVM (RESET RS);
}
. . .
} /*DO ITER*/
6.4 Remote references of REDUCTION type
6.4.1 Synchronous specification of remote references of REDUCTION type
If in a parallel loop REDUCTION specification hasn't group name, it is synchronous specification and executed in two steps.
6.4.2 Asynchronous specification of remote references of REDUCTION type
Asynchronous specification allows:
For asynchronous specification besides REDUCTION directive (with group name) the following additional directives are required.
| reduction-start-directive | ::= REDUCTION_START reduction-group-name |
| reduction-wait-directive | ::= REDUCTION_WAIT reduction-group-name |
Constraints.
Example 6.7. Asynchronous reduction of REDUCTION type.
DVM(REDUCTION_GROUP) void *RG;
. . .
S = 0;
X = A[1];
Y = A[1];
MINI = 1;
DVM(PARALLEL[I] ON A[I]; REDUCTION RG: SUM(S), MAX(X), MINLOC(Y,MIMI))
FOR(I, N)
{ S = S + A[I];
X =max(X, A[I]);
if(A[I] < Y) THEN { Y = A[I]; MINI = I;}
}
DVM(REDUCTION_START RG);
DVM(PARALLEL[I] ON B[I])
FOR( I, N)
B[I] = C[I] + A[I];
DVM(REDUCTION_WAIT RG);
printf("%f %f %f %d\n", S, X, Y, MINI);
While the reduction group is executed the values of array B elements will be computed.
DVM parallelism model joins data parallelism and task parallelism.
Task parallelism is implemented by independent computations processor arrangement sections.
Let us define a set of virtual processors, where a procedure is executed, as current virtual processor system. For main procedure the current system consists of total set of virtual processors.
The separate task group is defined by the following directives.
Several task array can be described in one procedure. Nested tasks are not allowed.
A task array is described by the following directive:
| task-directive | ::= TASK |
Task group description defines one-dimensional array of the tasks, which will be mapped then on the processor arrangement sections.
7.2 Mapping tasks on processors. MAP directive
The task mapping on processor arrangement section is performed by MAP directive
| map-directive | ::= MAP task-name [ task-index] |
| ONTO processors-name [ section-subscript-string ] |
Several tasks can be mapped on the same section, but different sections can not have common processors.
7.3 Array distribution on tasks
Array distribution over the tasks are performed by REDISTRIBUTE directives with the following extension:
| dist-target | ::= . . . |
| | task-name [ task-index ] |
The array is distributed on processor arrangement section, assigned to the task.
7.4 Distribution of computations. TASK_REGION directive
Distribution of statement blocks over the tasks is described by construction TASK_REGION:
| block-task-region | ::= DVM (task-region-directive ) { on-block ... } |
| task-region-directive | ::= TASK_REGION task-name |
| [ ; reduction-clause ] | |
| on-block | ::= DVM ( on-directive ) statement |
| on-directive | ::= ON task-name [ task-index ] |
Task region and each on-block are sequences of the statements with one entrance (the first statement) and one exit (after the last statement). For the statement blocks construction TASK_REGION is semantically equivalent to parallel section construction for shared memory systems. The difference is that the statement block can be executed on several processors in data parallel model.
A distribution of the parallel loop iterations on tasks is performed by the following construction:
| loop-task-region | ::= DVM ( task-region-directive ) { |
| parallel-task-loop | |
| } | |
| parallel-task-loop | ::= DVM ( parallel-task-loop-directive ) |
| do-loop | |
| parallel-task-loop-directive | ::= PARALLEL [ do-variable ] ON task-name [ do-variable ] |
Distributed computation unit is an iteration of one-dimensional parallel loop. The difference from usual parallel loop is the distribution of the iteration on the processor arrangement section, the section being defined by reference to the element of the task array.
Semantics of reduction-clause is the same as for paralle-loop-directive. Reduction variable value must be calculated in each task. After task completion (END TASK_REGION) in the case of synchronous specification the reduction over all values of reduction variable on all the tasks are automatically performed. In the case of asynchronous specification the reduction is started by REDUCTION_START directive.
7.5 Data localization in tasks
A task is on-block or loop iteration. The tasks of the same group have the following constraints on data
7.6 Fragment of static multi-block problem
The program fragment, describing realization of 3-block task (fig.6.2) is presented below.
DVM(PROCESSORS) void *P[NUMBER_OF_PROCESSORS()];
/* arrays A1,A2,A3 - the values on the previous iteration */
/* arrays A1,A2,A3 - the values on the current iteration */
DVM(DISTRIBUTE) float (*A1)[N1+1],(*A2)[N2+1],(*A3)N2+1];
DVM(ALIGN) float (*B1)[N1+1], (*B2)[N2+1], (*B3)[N2+1];
/* description of task array */
DVM(TASK) void *MB[3];
DVM (REMOTE_GROUP) void *RS;
. . .
/* distribution of tasks on processor arrangement */
/* sections and distribution of arrays on tasks */
/* (each section contain third of all the processors) */
NP = NUMBER_OF_PROCESSORS()/3;
DVM(MAP MB[1] ONTO P(0: NP-1));
A1=malloc(M*(N1+1)*sizeof(float));
DVM(REDISTRIBUTE A1[][BLOCK] ONTO MB[1]);
B1=malloc(M*(N1+1)*sizeof(float));
DVM(REALIGN B1[i][j] WITH A1[i][j]);
DVM(MAP MB[2] ONTO P( NP : 2*NP-1));
A2=malloc((M1+1)*(N2+1)*sizeof(float));
DVM(REDISTRIBUTE A2[][BLOCK] ONTO MB[2]);
B2=malloc((M1+1)*(N2+1)*sizeof(float));
DVM(REALIGN B2[i][j] WITH A2[i][j]);
DVM(MAP MB[3] ONTO P(2*NP : 3*NP-1));
A3=malloc((M1+1)*(N2+1)*sizeof(float));
DVM(REDISTRIBUTE A3[][BLOCK] ONTO MB[3]);
B3=malloc((M1+1)*(N2+1)*sizeof(float));
DVM(REALIGN B3[i][j] WITH A3[i][j]);
. . .
FOR(IT,MAXIT)
{. . .
DVM(PREFETCH RS);
/* exchanging edges of adjacent blocks */
. . .
/* distribution of statement blocks on tasks */
DVM(TASK_REGION MB)
{
DVM(ON MB[1]) JACOBY(A1, B1, M, N1+1);
DVM(ON MB[2]) JACOBY(A2, B2, M1+1, N2+1);
DVM(ON MB[3]) JACOBY(A3, B3, M2+1, N2+1);
} /* TASK_REGION */
} /* FOR */
7.7 Fragment of dynamic multi-block problem
Let us consider the fragment of the program, which is dynamically tuned on a number of blocks and the sizes of each block.
#define NA 20 /* NA - maximal number of blocks */
DVM(PROCESSORS) void *R[NUMBER_OF_PROCESSORS()];
int SIZE[2][NA]; /* sizes of dynamic arrays */
/* arrays of pointers for A and B */
DVM(* DISTRIBUTE) float *PA[NA];
DVM(* ALIGN) float *PB[NA];
DVM(TASK) void *PT[NA];
. . .
NP = NUMBER_OF_PROCESSORS( );
/* distribution of arrays on tasks */
/* dynamic allocation of the arrays */
/* and execution of postponed directives */
/* DISTRIBUTE and ALIGN */
FOR(i,NA)
{
DVM(MAP PT[I] ONTO R[ i%(NP/2) : i%(NP/2)+1] );
PA[i] = malloc(SIZE[0][i]*SIZE[1][i]*sizeof(float));
DVM(REDISTRIBUTE (PA[i])[][BLOCK] ONTO PT[I]);
PB[i] = malloc(SIZE[0][i]*SIZE[1][i]*sizeof(float));
DVM(REALIGN (PB[i])[I][J] WITH (PA[i])[I][J])
} /*FOR i */
. . .
/* distribution of computations on tasks */
DVM(TASK_REGION PT) {
DVM(PARALLEL[i] ON PT[i])
FOR(i,NA)
JACOBY(PA[i], PB[i], SIZE[0][i], SIZE[1][i]);
}
} /* TASK_REGION */
The arrays (blocks) are cyclically distributed on 2-processor sections. If NA > NP/2, then several arrays will be distributed on some sections. The loop iterations, distributed on the same section, will be executed sequentially in data parallel model.
Procedure call inside parallel loop.
A procedure, called inside parallel loop, must not have side effects and contains processor exchanges (purest procedure). As a consequence, the purest procedure doesn't contain nput/output statements and DVM-directives.
Procedure call outside parallel loop.
If the actual argument is explicitly distributed array (by DISTRIBUTE or ALIGN), it should be passed without shape changing. It means, that actual argument is the reference to the array beginning, and the actual and corresponding formal arguments have the same configuration.
Formal parameters.
If an actual parameter of a procedure may be a distributed array then corresponding formal parameter must be specified in the following way:
Local arrays.
In the procedure local arrays can be distributed by DISTRIBUTE and ALIGN directives. A local array can be aligned with formal parameter. The DISTRIBUTE directive distributes the local array on the processor subsystem, on which the procedure was called (current subsystem). If a processor arrangement section is specified in DISTRIBUTE directive, then the number of the processors must be equal to the number of processors of the current subsystem.
Example 9.1. Distribution of the local arrays and formal arguments.
void dist(
/* explicit distribution of formal argument */
DVM(*DISTRIBUTE[][BLOCK]) float *A /* N*N */,
/* aligned formal argument */
DVM(*ALIGN [i][j] WITH A[i][j]) float *B /* N*N */,
/* inherited distribution of the formal argument */
DVM(*) float *C /* N*N */ ,
int N)
{
DVM(PROCESSORS) void *PA[ACTIVE_NUM_PROC()];
/* local array aligned with formal argument */
DVM(ALIGN[I][J] WITH C[I][J]) float *X;
/* distributed local array */
DVM(DISTRIBUTE [][BLOCK] ONTO PA) float *Y;
}
Note. The sizes of actual parameter arrays are unknown. So the technique of dealing with dynamic multidimentional arrays described in section 4.2.3 should be used.
In C-DVM, the following I/O statements are allowed for replicated data:
fopen, fclose, feof, fprintf, printf, fscanf, fputc, putc, fputs, puts, fgetc, getc, fgets, gets, fflush, fseek, ftell, ferror, clearerr, perror, as well as fread, fwrite.
These statements are executed on the certain processor (input/output processor). Output values are taken from this processor, and input data are input on this processor and sent to others.
Only unformatted I/O of the whole array by fread/fwrite functions is allowed for distributed arrays.
The I/O functions cannot be used in a parallel loops and in TASK_REGION blocks. because output data will be written in the file (printed) in arbitrary order.
10 Restrictions on C language usage
C-DVM is intended for parallelization of computational programs, written in "Fortran-like" style. At that there are some restrictions on the usage of C language tools. First of all these restrictions concern the usage of the pointers to distributed arrays and their elements. C-DVM doesn't prohibit using the pointers, but some operations with them can become incorrect after the program conversion. For example:
The second restriction concerns data types: distributed array elements can have only scalar types int, long, float and double.
Then some descriptions require execution of certain actions for parallelization. They are, for example:
Such implicit actions for global objects are executed at the function main beginning immediately after Run-Time System initialization. Therefore at the time main function is generated all such objects must be known, that is they can't be located in separately compiled file or follow main function description. For objects, local in a function or in a program block, these actions are performed before first statement of the block. Moreover, note, that implicit actions are performed in the order of descriptions, and it causes certain semantic restrictions on the description order: the base of ALIGN must be described before aligned array and so on.
At last, preprocessor usage beyond header files requires a care for several reasons. First, C-DVM compiler operates before the preprocessor. So, for example, the pair of definitions
#define begin {
#define end }
can make the program absolutely not understandable for the compiler. For the same reason DVM-directives remain unknown to the compiler. Therefore, distributed data must be explicitly described in every file. Second, to deal with multidimensional arrays (see section 4.2) it is suggested to use the preprocessor for temporary redefinition of the array sizes as constants or for redefinition of the macrocomands, simulating multidimensional array via one-dimensional one. In converted program corresponding preprocessor directives must be excluded. It is implemented by placing all preprocessor directives in source order at the beginning of output file. (Note, that for every auxiliary directive #define the directive #undef, disabling it, is required.)
11 The difference between CDVM versions 1.0 and 2.0
CDVM 1.0 is a subset of CDVM 2.0. The following new possibilities are provided:
C-DVM language provides the tools for distributed array (distributed array section) copy, that allow to ensure overlapping data exchange with computations.
Rectangular array section is specified by triplets (<first>:<last>:<step>) for every dimension of array. For assignement both sections should be of the same rank, i.e. the same number of nonsingular dimensions (arrays themselves may be of different ranks), and should have the same number of elements in corresponding nonsingular dimensions of the source and destination sections.
In order to C-DVM program can be compiled and executed as usual sequential program, an array (array section) copy is written as ordinary multidimensional loop. The loop body should consist of a single assignement statement. The loop headers should be written by the DO(v,first,last,step) or FOR(v,times) macros. All the loop variables should be used in index expressions in right and left sides of the assignement statement, and in the same order. Every index expression may contain only one loop variable and should depend on it linearly.
For asynchronous copy it is neccessary:
Example 11.1. Asynchronous array copy.
DVM(DISTRIBUTE [BLOCK][]) float
A[N][N];
DVM(ALIGN [i][j] WITH [j][i]) float B[N][N];
. . .
DVM(COPY_FLAG) void * flag;
. . .
DVM(COPY_START &flag)
FOR(i,N)
FOR(j,N)
B[i][j]=A[i][j];
. . .
DVM(COPY_WAIT &flag);
If computation-communication overlapping is not required, it is possible slightly simplify the program using the synchronous copy directive COPY.
Example 11.2. Synchronous copy.
DVM(COPY)
FOR(i,N)
FOR(j,N)
B[i][j]=A[i][j];
Syntax rules.
| copy-flag-directive | ::= COPY_FLAG |
| copy-start-directive | ::= COPY_START flag_addr |
| copy-wait-directive | ::= COPY_WAIT flag_addr |
| copy-directive | ::= COPY |
| C-DVM - contents | Part 1(1-4) | Part 2 (5-11) | Part 3 (Appendixes) |