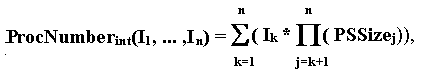
| Lib-DVM interface description (contents) | Part 1 (1-5) |
Part 2 (6-7) |
Part 3 (8-11) |
Part 4 (12-13) |
Part 5 (14-15) |
Part 6 (16-18) |
Part 7 (19) |
| created: february, 2001 | - last edited 03.05.01 - |
Before proceeding with DVM Run-Time Library functions let us give a short description of the parallel computations model. A parallel C-DVM (or Fortran DVM) program is translated to the program in the standard C (or Fortran 77) language extended by calls of the Run-Time Library functions, and to be executed according to SPMD model on each processor assigned to the task.
On startup the program has the only branch (control flow). This branch is executed from the first program statement on all the processors of the processor system.
Let us define the processor system (or system of the processors) as computing machine, assigned to the user program by hardware and by the base system software. For example, for computers with distributed memory the computing machine can be an MPI-machine. In this case, the processor system is a group of MPI-processes, created when the program is started. The number of the processors of processor system, as well as its representation as a multidimensional grid is specified in the command line starting the program. All declared variables are replicated over all the processors. The only exception is arrays specially defined as "distributed".
Entering a parallel loop, the branch is split into some number of parallel branches. Each of the branches is executed on a separate processor of the processor system.
Leaving a parallel construct, all parallel branches are merged into the original branch, which was executed before entering the parallel construct. At this moment all changes in replicated variables caused by the parallel branches execution become visible to all processors (that is, the variables are set to coherent state).
2 Run-Time System initialization and completion
Initialization in C program:
| long rtl_init ( | long int char |
InitParam, argc, *argv[] ); |
Initialization in Fortran program:
long linit_ (long *InitParamPtr);
| InitParam or *InitParamPtr |
- | parameter of Run-Time System initialization. |
| argc | - | number of string parameters in command line. |
| argv | - | array containing pointers to string parameters in command. |
The functions rtl_init and linit_ initializes Run-Time System internal structures according to modes of interprocessor exchanges, statistic and trace accumulation, and so on, defined in configuration files.
The initialization parameter can be:
| 0 | - | default initialization; |
| 1 | - | initialization with blocked dynamic control (in this case dynamic control specified in Run-Time System startup parameters is suppressed). |
The function returns zero.
long lexit_ (long *UserResPtr);
*UserResPtr - value returned by user program.
The function lexit_ completes correctly the execution of Run-Time System. That is, the function frees the memory used by Run-Time System, writes the statistic and trace information into disk file, and so on.
The function does not return control.
Note. A user program startup on processor system requires to specify (as startup parameters) the following characteristics of the processor system as multidimensional array: the processor system rank and sizes of all its dimensions.
Let the rank of processor system be n, and size of k-th dimension be PSSizek (1 £ k £ n). Then when Run-Time System is initializes an internal number ProcNumberint will be assigned to the each processor
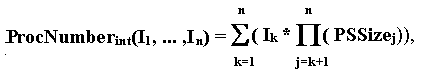
where:
| Ik | - | processor index value of k-th dimension of the processor system index space (0 £ Ik £ PSSizek - 1). |
So the internal number is the linear index of the processor in index space of the procåssor system.
In interprocessor exchanges a processor identifier ProcIdent is used as the processor adsress. The correspondence
ProcNumberint => ProcIdent
is defined by Message Passing System and returned to Run-Time System when it is initialized.
There are two functionally special processors: input/output processor and central processor among processors, assigned to a task. Input/output processor is intended to deal with the file system directly (see section 16) and its internal number is zero. The central processor computes the reduction functions (see section 11) and is defined by an index vector ([PSSize1/2], ... ,[PSSizen/2]).
3 Creating abstract machine representations
An abstract machine concept is introduced for two-step mapping of a parallel program onto a real parallel computer. First, a programmer creates an abstract machine, most suitable for his program (that is, the abstract machine realizing all potential program parallelism). Then, the programmer defines the mapping of his computations and data onto this machine, and he also defines the rules of mapping this abstract machine onto a real parallel computer. Therefore, an abstract machine is a hierarchy of abstract parallel subsystems. Each of these subsystems can be represented as a multidimensional array of subsystems of the next hierarchy level. Several different representations for each subsystem may co-exist.
There is no an "abstract machine" notion in C-DVM and Fortran-DVM languages. Instead of that the term "template" ("TEMPLATE") is used. Each "template", described in the program, is represented as abstract machine in Run-Time System. For each explicitly distributed array (that is array, specified with DVM-directive "DISTRIBUTE") a corresponding abstract machine is created too.
3.1 Requesting current abstract machine
AMRef getam_(void);
This function returns a reference to current abstract machine. The current abstract machine is an abstract machine the current program branch is mapped on. Only one abstract machine (the top level of hierarchy) exists when the program starts. The initial abstract machine is mapped onto the processor system assigned by Operating System (OS) for program execution. Therefore, all processors concerned execute initial program branch (mapped onto initial abstract machine). All abstract machines, which program creates later, are descendants of the initial abstract machine. An abstract machine becomes the current one when control enters parallel branch (subtask or parallel loop iteration) mapped onto this abstract machine or when control exits from the parallel construct.
3.2 Creating abstract machine representation
| AMViewRef crtamv_ ( | AMRef long long long |
*AMRefPtr, *RankPtr, SizeArray[], *StaticSignPtr ); |
||
| *AMRefPtr | - | a reference to the abstract machine. | ||
| *RankPtr | - | a rank of created representation. | ||
| SizeArray | - | array, which i-th element is a size of the (i+1)-th dimension of the created representation (0 £ i £ *RankPtr - 1). | ||
| *StaticSignPtr | - | the flag of static representation creation. | ||
The function crtamv_ creates a representation of the assigned abstract machine as an array of abstract machines of the next hierarchy level. The function returns reference to the created representation. The representation of the abstract machine as an array allows data arrays and parallel constructs to be mapped onto the abstract machine. An abstract machine can possess several representations, and each of them being an array of abstract machines of the next hierarchy level.
Parental abstract machine, specified by *AMRefPtr reference must be the current abstract machine or its (direct or indirect) descendant. If AMRefPtr = NULL or *AMRefPtr = 0, a representation of the current abstract machine will be created.
If the flag *StaticSignPtr of static representation is not equal to zero, then the created representation will not be deleted automatically, when the control exits the program block (see section 8). Such type of representation can be deleted only explicitly using the function delamv_ considered below.
3.3 Requesting reference to an element of abstract machine representation
| AMRef getamr_ ( | AMViewRef long |
*AMViewRefPtr, IndexArray[] ); |
||
| *AMViewRefPtr | - | a reference to the abstract machine representation. | ||
| IndexArray | - | array, which i-th element is a index value of requested element (that is abstract machine) along (i+1)-th dimension. | ||
The size of the array IndexArray must be equal to the rank of specified representation of the abstract machine.
3.4 Deleting abstract machine representation
long delamv_(AMViewRef *AMViewRefPtr);
*AMViewRefPtr – the reference to the abstract machine representation.
The function deletes an abstract machine representation, created by the function crtamv_. When the representation is deleted, all representations of the abstract machines, included in the representation and all distributed arrays mapped on the representation are deleted aìso.
After deleting the representation the reference can be used by user program for its own goals.
A representation of abstract machine can be deleted by delamv_ function only if it was created in the current subtask and in the current program block (or in its subblock) (see sections 8 and 10).
To delete an abstract machine representation the function delobj_ can also be used (see section 17.5).
The function returns zero.
4.1 Requesting reference to the processor system
PSRef getps_ (AMRef *AMRefPtr);
*AMRefPtr – a reference to the abstract machine.
The function getps_ returns a reference to the processor system the specified abstract machine is mapped onto. The parameters of the processor system (the rank and the size of each dimension) can be obtained through the functions getrnk_ and getsiz_ (see section 17).
If AMRefPtr = NULL or *AMRefPtr = 0 the reference to the processor system, the current abstract machine is mapped on, is returned (i.e. the reference on the current processor system is returned).
If *AMRefPtr = –1, the function returns the reference to initial processor system.
The returned reference will be equal to zero, if specified abstract machine is not mapped on any processor system.
4.2 Creating subsystem of specified processor system
| PSRef crtps_ ( | PSRef long long long |
*PSRefPtr, InitIndexArray[], LastIndexArray[], *StaticSignPtr ); |
||
| *PSRefPtr | - | reference to the (source) processor system whose subsystem will be created. | ||
| InitIndexArray | - | array, which i-th element is an initial value of the index of the (i+1)-th dimension of the source processor system. | ||
| LastIndexArray | - | array, which i-th element is last value of the index of the (i+1)-th dimension of the source processor system. | ||
| *StaticSignPtr | - | the flag of the static subsystem creation. | ||
The function crtps_ creates the subsystem of the same rank, as the rank of source processor system, and returns the reference to the subsystem. The sizes of InitIndexArray and LastIndexArray arrays must be equal to the rank of the source (and to be created) processor systems.
All processors of source processor system, specified by *PSRefPtr reference, must be the members of the current processor system. If the pointer PSRefPtr is equal to NULL or the reference *PSRefPtr has a zero value then the current processor system will be used as source one.
Internal values of element coordinates of any processor system are numbered from 0. Therefore element (P1, ... , Pj, ... , Pn) of the created processor subsystem is the element (P1+InitIndexArray[0], ... , Pj+InitIndexArray[j-1], ... , Pn+InitIndexArray[n-1]) of the source processor system (n is the rank of source and created systems). The size of i-th dimension of the created subsystem is equal to LastIndexArray[i-1]-InitIndexArray[i-1]+1.
If the flag *StaticSignPtr of static processor subsystem is not equal to zero, then the created processor system will not be deleted automatically, when the control exits the program block (see section 8). Such subsystem can be deleted only explicitly using the function delps_ considered below.
Computational coordinate weights of created subsystem processors will be set to 1.
Note, that processor systems, created by crtps_ function, can be intersected by processors.
4.3 Reconfiguring (changing shape of) processor system
| PSRef psview_ ( | PSRef long long long |
*PSRefPtr, *RankPtr, SizeArray[], *StaticSignPtr ); |
|
| *PSRefPtr | - | reference to the source (to be reconfigured) processor system. | |
| *RankPtr | - | rank of the target (reconfigured) processor system. | |
| SizeArray | - | array, which i-th element is the size of (i+1)-th dimension of the target processor system. | |
| *StaticSignPtr | - | flag of static target processor system. | |
The function psview_ creates new processor system from the elements of the source processor system and returns reference to the target system. A number of elements in the source and target systems must be the same.
All processors of source processor system, specified by *PSRefPtr reference, must be members of the current processor system. If the pointer PSRefPtr is equal to NULL or the reference *PSRefPtr has a zero value then the current processor system will be used as source one.
Computational coordinate weights of created subsystem processors will be set to 1.
long delps_ (PSRef *PSRefPtr);
*PSRefPtr - reference to the processor system to be deleted.
The function deletes the processor system, created by the function crtps_ (or psview_). When the processor system is deleted, all its subsystems and all mapped on the processor system representations of abstract machines and distributed arrays are deleted also. Abstract machines, mapped on deleted processor system by mapam_ function are not deleted, but the subtasks, created by the function, will not exist (see section 10).
The processor system can be deleted by delps_ function only if it was created in the current subtask and in the current program block (or in its sub-block) (see sections 8 and 10). Initial processor system can't be deleted.
To delete a processor system the function delobj_ can also be used (see section 17.5).
The function returns zero.
4.5 Weights of processor system elements
Let a processor system be n-dimension array, and a function WEIGHTi with the domain of definition in a space of values of i-th dimension index variable and with image in real numbers, more or equal to 1 be defined for every dimension. A value of function WEIGHTi(Pi) will be called the weight of Pi coordinate (1 £ i £ n , 0 £ Pi < PSSIZEi , PSSIZEi is a size of i-th dimension of processor system).
Then processor (P1, ... , Pi, ... , Pn) weight is by definition
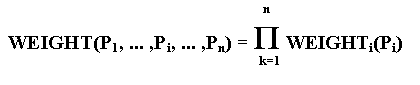
The coordinate weights of the initial processor system elements (therefore and processor weights) are parameters of Run-Time System startup. When a user program is running the coordinate weights of the processors of the processor system can be assigned (changed) by the function
| long setpsw_( | PSRef AMViewRef double |
*PSRefPtr, *AMViewRefPtr, CoordWeightArray[] ); |
||
| *PSRefPtr | - | reference to the processor system, whose element coordinate weights will be assigned. | ||
| *AMViewRefPtr | - | reference to the abstract machine representation, to be mapped onto specified processor system with the assigned coordinate weights. | ||
| CoordWeightArray | - | array, containing processor coordinate weights. | ||
Depending on AMViewRefPtr parameter value there are two ways of setpsw_ function execution.
1. AMViewRefPtr ¹ NULL and *AMViewRefPtr ¹ 0.
Assigned weights of processor coordinates are intended only for mapping or remapping given representation of abstract machine on given processor system.
When setpsw_ function is called the abstract machine (parental) with representation, specified by *AMViewRefPtr reference, must be already mapped.
All processors of the system, specified by *PSRefPtr reference, must belong to elementary intersection of the current processor system with the processor system, the parental abstract machine is mapped on. NULL value of PSRefPtr pointer or zero value of *PSRefPtr reference means, that coordinate weights of the current processor system elements are assigned.
2. AMViewRefPtr = NULL or *AMViewRefPtr = 0.
Assigned weights of processor coordinates, as the weights, specified at Run-Time System startup, will be used in mapping or remapping of all representations of abstract machines on given processor system (except ones, for those their own procåssor coordinate weights were assigned or will be assigned by setpsw_ function).
All processors of system, specified by *PSRefPtr reference, must be the members of the current processor system. NULL value of PSRefPtr pointer or zero value of *PSRefPtr reference means, that coordinate weights of the current processor system elements are assigned.
The weight of coordinate Pi is specified by a value of
| i-1 |
| (å PSSIZEk + Pi)-th |
| k=1 |
element of the array CoordWeightArray. A number of elements of the array CoordWeightArray, containing processor coordinate weights, must be equal to sum of sizes of all processor system dimensions. The coordinate weights in the array CoordWeightArray may be any positive numbers. Executing function setpsw_, Run-Time System updates every weight Pi dividing it by minimal weight of the coordinate in the array CoordWeightArray.
If CoordWeightArray = NULL or CoordWeightArray[0] = 0, then coordinate weights, specified in Run-Time System startup parameters, are used as assigned coordinate weights (for initial processor system; for not initial processor system in this case coordinate weights will be set to 1).
If CoordWeightArray [0] = - 1, then the weights of all coordinates will be set to 1 and will not be updated later, i.e. they will be considered as optimal weights of processor coordinates (see below).
The function returns zero.
The processor coordinate weights, considered above, are called computational weights. They determine distribution of data and computations over processors: computational processor loading is proportional to computational weight of the processor (equal to product of computational weights of its coordinates). The computational weights of the processor coordinates reflect calculation heterogeneity of the task being solved and are specified so that to provide balanced processor loading under condition, that they have the same performances.
A difference in processor performance is specified by performance weights: the processor performance is proportional to its performance weight. The performance weights (real numbers, equal to or more than 1) are Run-Time System startup parameters and cannot be updated by a user program.
When Run-Time System is initialized (and when the function setpsw_ is executed) computational weights of processor coordinates are updated according to the processor performance. The result of updating is optimal weights of the processor coordinates, reflecting as calculation heterogeneity of the task being solved as hardware heterogeneity of the processor system. The optimal weights provide the best balance of computations and are specified as follows. Let:
| WEIGHTcalc,i (Pi) | - | computational weight of Pi coordinate of the processor system (specified under assumption that performance weights of all the processors are equal to 1; |
| WEIGHTperf (P1, ... , Pi, ... , Pn) | - | performance weight of the processor element (P1, ... , Pi, ... , Pn); |
| WEIGHTopt,i (Pi) | - | optimal weight of coordinate Pi of the processor system i-th dimension. |
Let us suppose, that processor weight, determining the processor loading by data and computations is:
Let us suppose also, that "contribution" of processor performance weight into its coordinate weights is the same.
Therefore a value of processor performance weight WEIGHTperf(P1, ... , Pi, ... , Pn) requires to increment the computational weight of any its coordinate by WEIGHTperf1/n(P1, ... , Pi, ... , Pn) times.
Since when optimal weight of coordinate Pi is calculated it is necessary to take into account the performance weights of all the processors with coordinate Pi, required weight WEIGHTopt,i(Pi) for any Pi must be a solution of the following optimization task (criterion is best balanced processor loading):
| MAX ( abs( WEIGHTopt,i(Pi) - | WEIGHTperf1/n(P1, ... ,Pi, ... Pn) * |
| 0 £
p1 < pssize1 . . . . . . .. . . . . . .. 0 £ pi-1 < pssizei-1 0 £ pi+1< pssizei+1 . . . . . . .. . . . . . .. 0 £ pn < pssizen |
WEIGHTcalc,i(Pi) ) ) à MIN |
The solution in domain of real numbers, more than or equal to 1, is
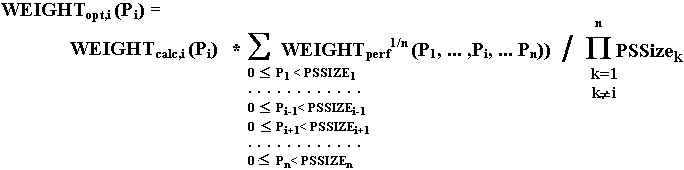
Using optimal weights of processor coordinates for non-uniform distribution of the elements of abstract machine representation (and as consequence, the elements of distributed array and parallel loop iterations) is considered in section 5.7.
Besides setpsw_ function considered above, computational processor coordinate weights can be assigned by the functions
| long genbli_( | PSRef AMViewRef AddrType long |
*PSRefPtr, *AMViewRefPtr, AxisWeightAddr[], *AxisCountPtr ); |
and
| long genbld_( | PSRef AMViewRef AddrType long |
*PSRefPtr, *AMViewRefPtr, AxisWeightAddr[], *AxisCountPtr ); |
The parameters PSRefPtr and AMViewRefPtr of the functions are similar to the same named parameters of setpsw_ function. Processor coordinate weights are set in an array, individual for every dimension of the processor system. The array address is contained in AxisWeightAddr array: i-th element of AxisWeightAddr array is the pointer, cast to AddrType, to the array, containing processor coordinate weights of (i+1)-th dimension of the specified processor system. The function genbli_ assumes that processor coordinate weights are represented as positive integer numbers (integer), and the function genbld_ - positive float numbers (double).
Zero value of AxisWeightAddr[i] means, that for (i+1)-th dimension of the processor system the processor coordinate weights will be equal to the weights, specified in Run-Time System startup parameters (for initial processor system), or to 1 (for other one).
*AxisCountPtr parameter (non-negative integer) defines a number of AxisWeightAddr array elements. Its value can't exceed specified processor system rank. AxisWeightAddr array elements, lacking up to the processor system rank, will be assumed equal to null. In particular, zero value of *AxisCountPtr means, that the weights of all coordinates of all the processors will be set equal to 1 or to the weights, specified in Run-Time System startup parameters.
The functions return zero values.
Note. genbli_ and genbld_ functions just call the function
| long genblk_( | PSRef AMViewRef AddrType long long |
*PSRefPtr, *AMViewRefPtr, AxisWeightAddr[], *AxisCountPtr, *DoubleSignPtr ); |
First four parameters of the function are identical to same named parameters of genbli_ and genbld_ functions, and last one, *DoubleSignPtr is non-zero flag to represent processor coordinate weights as positive float numbers (double).
4.6 Specifying coordinate weights of processors using their loading weights
| long setelw_ ( | PSRef AMViewRef AddrType long long |
*PSRefPtr, *AMViewRefPtr, LoadWeightAddr[], WeightNumber[], *AddrNumberPtr ); |
|
| *PSRefPtr | - | reference to the processor system, for which elements coordinate weights will be set. | |
| *AMViewRefPtr | - | reference to abstract machine representation, to map which the coordinate weights, computed by setelw_ function, will be used. | |
| LoadWeightAddr | - | array, which i-th element is cast to AddrType type pointer to the array containing coordinate weights of processor loading for (i+1)-th dimension of the processor system, specified by *PSRefPtr reference. | |
| WeightNumber | - | array, which i-th element is the number of elements (coordinate weights of loading) in the array, the pointer on which is specified in LoadWeightAddr[i]. | |
| *AddrNumberPtr | - | a number of elements in LoadWeightAddr and WeightNumber arrays. | |
The function setelw_ calculates computational coordinate weights of elements of the processor system, specified by *PSRefPtr reference and then assigns them using genbld_ function (see section 4.5).
Assigned weights of processor coordinates will be used only for mapping or remapping given representation of abstract machine on given processor system.
When setelw_ function is called the abstract machine (parental) with representation, specified by *AMViewRefPtr reference, must be already mapped.
All processors of the system, specified by *PSRefPtr reference, must belong to elementary intersection of the current processor system with the processor system, the parental abstract machine is mapped on.
NULL value of PSRefPtr pointer or zero value of *PSRefPtr reference means, that coordinate weights of the current processor system elements are assigned.
The computational weights of the processor coordinates are defined so that to provide best balanced processor loading: for each dimension of given processor system maximal coordinate loading of the processors must be minimal.
Formally, for each (i+1)-th dimension of given processor system setelw_ function solves the task (relative to Ik,init and Ik,last)
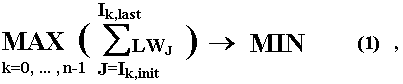
where:
| N | - | size of (i+1)-th dimension of given processor system; |
| Ik,init £ Ik,last; | ||
| Ik+1,init = Ik,last + 1; | ||
| I0,init = 0, | In-1,last = m - 1; | |
| m | - | a number of loading coordinate weights, specified for (i+1)-th dimension of the processor system (WeightNumber[i]); m ³ n); |
| LWJ | - | J-th loading coordinate weight, specified for (i+1)-th dimension of processor system (J-th element of the array which pointer is specified in LoadWeightAddr[i]). |
After finding the task (1) solution (denote it as Ik,init,even , Ik,last,even; k = 0, ... , n-1) computational weight of k-th coordinate of (i+1)-th dimension of specified processor system will be equal to
Ik,last,even - Ik,init,even + 1 (k = 0, ... , n - 1).
Loading coordinate weights must be non-negative float numbers (double).
Zero value of LoadWeightAddr[i] means, that for (i+1)-th dimension of the specified processor system processor coordinate weights will be equal to the weights, specified in Run-Time System startup parameters (for initial processor system), or to 1 (for other one).
*AddrNumberPtr parameter value can't exceed specified processor system rank. LoadWeightAddr array elements, lacking up to the processor system rank, will be equal to zero. In particular, zero value of *AddrNumberPtr means, that the weights of all coordinates of all the processors will be set equal to 1 or to the weights, specified in Run-Time System startup parameters.
The function returns zero.
4.7 Virtual processor systems (processor systems of user program)
User program can be "strongly" tuned on certain initial processor system optimal for it. To support the program execution on other processor configuration, Run-Time system provides mechanism of virtual processor systems.
Mechanism of virtual processor systems allows using as fixed initial processor system of the program virtual processor system. equivalent to it (processor systems are equivalent, if they have the same rank and equal sizes of dimensions with equal numbers. The ranks of real and virtual initial processor systems must be the same, but sizes of their dimensions with equal numbers may differ. The amounts of processors in these processor systems may also differ.
Virtual initial processor system is described in Run-Time system startup parameter files by the directive
UserPS = <list of dimension sizes via comma>;
The rank of processor system, specified by the directive, is equal to a number of dimension sizes in the list.
To start program on virtual initial processor system non-zero value (1) should be assigned to Run-Time system startup parameter IsUserPS.
In this case:
So, when the program is executed on virtual processor systems, abstract machine representations and therefore distributed arrays and parallel loops can be mapped on virtual processor system only by equal blocks (see section 5.7).
Note. If a program is "strongly" tuned only on a number of processors in initial processor system (but not on the sizes of its dimensions), it is recommended to describe virtual initial processor system as one-dimensional.
5.1 Mapping abstract machine representation onto processor system (resource distribution)
| long distr_ ( | AMViewRef PSRef long long long |
*AMViewRefPtr, *PSRefPtr, *ParamCountPtr, AxisArray[], DistrParamArray[] ); |
||
| *AMViewRefPtr | - | reference to abstract machine representation, which resources will be distributed. | ||
| *PSRefPtr | - | reference to the processor system, which defines the structure of the distributed resources. | ||
| *ParamCountPtr | - | the number of parameters defined in arrays AxisArray and DistrParamArray (see below). | ||
| AxisArray | - | array, which j-th element is a dimension number of the abstract machine representation used in mapping rule for processor system (j+1)–th dimension. | ||
| DistrParamArray | - | array, which j-th element is a mapping rule parameter for processor system (j+1)-th dimension (DistrParamArray[j] ³ 0). | ||
The processor resource (the resource) of the abstract machine is a set of processors, which forms the processor system the abstract machine is mapped onto.
The function distr_ distributes resources of the ábstract machine among child abstract machines, and the reference *AMViewPtr defines the representation containing these abstract machines. Such distribution is called mapping of abstract machine representation on processor system. The abstract machine representation can be mapped only if it was created in the current subtask (see section 10).
When distr_ function is called the abstract machine (parental) which representation is passed in the function call, must be already mapped. All processors of the system, specified by *PSRefPtr reference, must belong to elementary intersection of the current processor system and the processor system, the parental abstract machine is mapped on. If *PSRefPtr = 0 or PSRefPtr = NULL, the current processor system will be used for resource distribution.
It is impossible to map the abstract machine representation, already mapped by distr_ (redis_, mdistr_, mredis_) function or the representation, where at least one element is mapped on some processor system by mapam_ function (see section 10).
The size of vectors PSAxisArray and DistrParamArray must be equal to *ParamCountPtr, which is equal to or less than the rank of the processor system. In the latter case missing rules are considered as replicating mapping rules (see the rule 2 below).
The following functional correspondence defines abstract machine resource distribution
{abstract machine representation} Þ {processor system} ,
which is performed as described below. Let F be a multifunction, with the domain of definition in a space of indexes of the abstract machine representation and with the image in a space of indexes of the processor system:
| F((I1, ... , Ii, ... , In)) = | F1(I1,
... , Ii, ... , In)
´ . . . . . . . . . . . . . . . Fj(I1, ... , Ii, ... , In) ´ . . . . . . . . . . . . . . . Fm(I1, ... , Ii, ... , In) |
where:
| ´ | - | symbol of the Cartesian product; |
| n | - | rank of the abstract machine; |
| m | - | rank of the processor system; |
| Ii | - | index variable of the i-th dimension of the abstract machine representation; |
| Fj | - | multifunction with an image in a set of index variable values of the processor system j-th dimension. |
Let the child abstract machine be defined by index vector (I1, … , In). Then the resource, which will be assigned to this abstract machine, is processor aggregate defined by set F((I1, ... , In)) (the values of these functions are sets consisting of vectors of the index space of the processor system). Mapping the representation of the abstract machine onto processor system is a resource distribution (through specification of function F) among components of this representation.
The F1, ... , Fm functions are named "coordinate mapping rules". Run-Time System provides the following mapping rules that allow realizing some block distribution of the abstract machine representation onto the processor system.
1. Fj(I1, ... ,In) = {[Ik/BLSIZEk]} , where:
| k = f(j) = AxisArray[j-1] | - | the dimension number of the abstract machine representation (1 £ k £ n, f(j1) ¹ f(j2) when j1 ¹ j2); |
| BLSIZEk | - | positive integer (the block size of the k-th dimension of the abstract machine representation). |
This mapping rule means that for each element (I1, … , In) of the index space of the abstract machine representation the corresponding image-set contains one element [Ik/BLSIZEk]. This element is within the values range of index variable of the j-th dimension of the processor system.
The BLSIZEk value is determined as follows. Let:
| AMSIZEk | - | the size of the k-th dimension of the abstract machine representation; |
| PSSIZEj | - | the size of the j-th dimension of the processor system. |
Then:
| BLSIZEk = { | min(DistrParamArray[j-1],
AMSIZEk) if DistrParamArray[j-1] ¹ 0; (AMSIZEk-1) / PSSIZEj] + 1 if DistrParamArray[j-1] = 0. |
Note, that the maximum value of Ik is
min( (PSSIZEj * BLSIZEk - 1) , AMSIZEk - 1 ).
Therefore, to use the mapping rule for the whole range of the k-th dimension of the abstract machine representation the following is required:
AMSIZEk £ PSSIZEj * BLSIZEk ,
that is true, when
DistrParamArray[j-1] ³ AMSIZEk
/ PSSIZEj
or when
DistrParamArray[j-1] =
0.
2. Fj(I1, ... , In) = {q Î Mj: 0 £ q £ PSSIZEj-1} , where:
| Mj | - | range of values of the index variable of the processor system j-th imension. |
This mapping rule means that for each element (I1, …, In) of index space of the abstract machine representation the corresponding image-set consists of the whole range of values of the index variable of the processor system j-th dimension. In such a case, the symbol "*" ("any of the admissible") is usually used.
3. Fj(I1, ... , In) = { Const } , where 0 £ Const £ PSSIZEj-1 .
This mapping rule means that for each element (i1, …, in) of index space of the abstract machine representation the corresponding image-set contains one element Const belonging to the range of values of the index variable of the processor system j-th dimension.
As a result of mapping of specified representation of parental abstract machine on specified processor system, performed by distr_ function, every element of the representation (i.e. descendant abstract machine) will be matched with a processor system (a set of processors, which is an image of the representation element for F mapping function considered above). The abstract machine together with its processor image forms parallel subtask. The subtask is activated (started) when control enters corresponding parallel loop iteration. The subtask execution is parallel loop iteration execution (see section 9). Another way of parallel subtask creation and startup is considered in section 10.
Examples.
| AM[9][8] | (0 £ I1 £ 8 , 0 £ I2 £ 7); |
| PS[3][4] | (0 £ J1 £ 2 , 0 £ J2 £ 3). |
Then the function F( (I1,I2)
) = {[I1/3]} ´ {[I2/2]}
sets the following correspondence:
element PS[j1][j2]
Û sub-matrix
AM[3*j1 £
I1 £
3*j1 + 2][2*j2
£ I2
£ 2*j2
+ 1] (block [3][2]).
| AM[12] | (0 £ I £ 11); |
| PS[4][3] | (0 £ J1 £ 3 , 0 £ J2 £ 2). |
Then the function F( (I) ) = {2} ´ {[I/4]} sets the
following correspondence:
element PS[2][j2] Û vector AM[4*j2
£ I £ 4*j2 +
3] (block [4]).
The image of F does not include rows 0, 1 and 3 of
the processor system.
| AM[8][12] | (0 £ I1 £ 7 , 0 £ I2 £ 11); |
| PS[3] | (0 £ J £ 2). |
Then the function F( (I1,I2)
) = {[I2/4]} sets the
following correspondence:
element PS[j] <=>
sub-matrix AM[0 £
I1 £
7][4*j £ I2
£ 4*j + 3]
(block [8][4]).
| AM[12] | (0 £ I £ 11); |
| PS[4][3] | (0 £ J1 £ 3 , 0 £ J2 £ 2). |
Then the function F( (I) ) = {*} ´ {[I/4]} sets the
following correspondence:
element PS[j1][j2]
<=> vector AM[4*j2
£ I £ 4*j2 +
3] (block [4]).
That is, the image of F from the b) example is
replicated along rows of the processor system.
| AM[9][8] | (0 £ I1 £ 8 , 0 £ I2 £ 7); |
| PS[3][4] | (0 £ J1 £ 2 , 0 £ J2 £ 3). |
Then the function F( (I1,I2)
) = {*} ´ {*} sets
the following correspondence:
element PS[j1][j2]
<=> sub-matrix AM[0 £ I1
£ 8][0 £ I2
£ 7] (block
[9][8]),
that is the whole space of the abstract machine
representation.
Note. If an abstract machine representation from an example e) is given as template for the function align_ (realn_), then fully replicated distributed array (each element of an array is represented on each virtual processor, see section 7.1) can be obtained.
When the function distr_ is called, the coordinate mapping rule Fj(I1, ... , In) = { [Ik/BLSIZEk] } for j-th dimension of the processor system is defined as following:
| AxisArray[j-1] | contains value k; |
| DistrParamArray[j-1] | contains value BLSIZEk. |
If DistrParamArray[j-1] is equal to zero, then Run-Time System evaluates BLSIZEk as described above.
To specify rule Fj(I1, ... , In), with image in set of all values of index variable of j-th dimension of processor system for any I1, ... , In, value AxisArray[j-1] (value k) must be set to zero. The value DistrParamArray[j-1] is irrelevant in this case.
The mapping rule Fj(I1, ... , In) = { Const } is defined as follows:
| AxisArray[j-1] | = -1; |
| DistrParamArray[j-1] | contains value Const. |
The function returns non-zero, if mapped representation has local part on current processor, and zero in other case.
5.2 Remapping abstract machine representation onto processor system (resource redistribution)
| long redis_ ( | AMViewRef PSRef long long long long |
*AMViewRefPtr, *PSRefPtr, *ParamCountPtr, AxisArray[], DistrParamArray[], *NewSignPtr ); |
||
| *AMViewRefPtr | - | reference to the parental abstract machine representation, which mapping has to be redistributed. | ||
| *PSRefPtr | - | reference to the processor system, which defines resource structure of a new distribution. | ||
| *ParamCountPtr | - | the number of parameters, defined in arrays AxisArray and DistrParamArray. | ||
| AxisArray | - | array, which j-th element is a dimension number of the abstract machine representation used in the mapping rule for processor system (j+1)-th dimension. | ||
| DistrParamArray | - | array, which j-th element is a mapping rule parameter for parallel system (j+1)-th dimension (DistrParamArray[j] is a nonnegative integer). | ||
| *NewSignPtr | - | the flag that defines whether to save contents of realigned arrays or not. | ||
The function redis_ cancels the resource distribuôion of the parental abstract machine previously defined for child abstract machines from *AMViewRefPtr representation by the function distr_ (or mdistr_ , see section 5.4). The function defines new distribution of this representation according to specified parameters. All the distributed arrays aligned with this representation by the function align_ and malign_ (whether directly or not), are remapped according to old alignment rules (see section 7).
The contents of redistributed arrays, depending on *NewSignPtr value, will be
If NewSignPtr = 1 all redistributed arrays will be nevertheless cleared by "zero" byte, if Run-Time system was started with non-zero DisArrayFill parameter (sysdebug.* files of base parameter sets).
When the arrays are remapped, the values of their shadow edges (see section 12) are not kept.
All elements of specified representation must be terminals of abstract machine hierarchy (must not have descendants).
All processors of the system, specified by *PSRefPtr reference, must belong to elementary intersection of the current processor system and the processor system, the parental processor system is mapped on. If *PSRefPtr = 0 or PSRefPtr = NULL, the current processor system will be used for resource distribution.
Remapped representation may be specified indirectly, if a header of distributed array, created by the function crtda_ with parameter *ReDistrParPtr equal to 1 or 3, is used as parameter *AMViewRefPtr (see section 6).
The abstract machine representation, passed in the function call, can be not mapped earlier. In this case redis_ function is executed as distr_ function, and *NewSignPtr parameter value is irrelevant.
The function returns non-zero, if remapped representation has a local part on the current processor, and zero in the other case.
| AMViewMapRef amvmap_ ( | AMViewRef long |
AMViewRefPtr, *StaticSignPtr ); |
||
| *AMViewRefPtr | - | reference to the abstract machine representation. | ||
| *StaticSignPtr | - | flag of static map creation. | ||
The function amvmap_ creates an object (a map), describing the current mapping of abstract machine representation onto the processor system, and returns a reference to the created object.
The map of the abstract machine representation contains in particular the following information:
If flag of static map *StaticSignPtr is not equal to zero, then the map will not be deleted when control exits a program block (see section 8). Such map can be deleted only explicitly by the function delmvm_ considered in section 5.6.
5.4 Specifying abstract machine representation mapping according to map
| long mdistr_ ( | AMViewRef PSRef AMViewMapRef |
*AMViewRefPtr, *PSRefPtr, *AMViewMapRefPtr ); |
||
| *AMViewRefPtr | - | reference to the abstract machine representation to be mapped. | ||
| *PSRefPtr | - | reference to the processor system, determining distributed resource structure. | ||
| *AMViewMapRefPtr | - | reference to the map of the abstract machine representation. | ||
The function mdistr_ specifies mapping the abstract machine representation onto specified processor subsystem according to the map.
When mdistr_ function is called, abstract machine (parental), which representation is specified by *AMViewRefPtr reference, must be already mapped.
If PSRefPtr is NULL or *PSRefPtr is zero, then the subsystem, whose reference is in the map, will be used as the processor subsystem.
All processors of the system, specified by *PSRefPtr reference or by a reference, contained in the map, must belong to elementary intersection of the current processor system and the processor system, the parental abstract machine is mapped on.
The ranks of the abstract machine representation and the processor subsystem must be equal to the corresponding ranks in the map.
It is impossible to map the abstract machine representation, already mapped by distr_ (redis_, mdistr_, mredis_) function or the representation, where at least one element is mapped on some processor system by mapam_ function (see section 10).
The function returns non-zero, if remapped representation has a local part on the current processor, and zero in the other case.
5.5 Remapping abstract machine representation according to the map
| long mredis_ ( | AMViewRef PSRef AMViewMapRef long |
AMViewRefPtr, *PSRefPtr, *AMViewMapRefPtr, *NewSignPtr ); |
||
| *AMViewRefPtr | - | reference to abstract machine representation to be remapped. | ||
| *PSRefPtr | - | reference to the processor system, determining resource structure for new mapping. | ||
| *AMViewMapRefPtr | - | reference to map of the abstract machine representation. | ||
| *NewSignPtr | - | flag of renewing all redistributed arrays (if it is equal to 1). | ||
The function mredis_ cancels resource distribution of the abstract machine, implemented earlier by the function mdistr_ (or distr_, see section 5.1) for descendant abstract machines, included to the representation, specified by reference *AMViewRefPtr, and redistributes the given representation according to specified map. All distributed arrays, aligned earlier with the considered representation by the functions align_ and malign_ (as explicitly as implicitly) will be remapped according to the old aligning rules (see section 7).
The contents of redistributed arrays, depending on *NewSignPtr, will be
If NewSignPtr = 1 all redistributed arrays will be nevertheless cleared by "zero" byte, if Run-Time system was started with non-zero DisArrayFill parameter (sysdebug.* files of base parameter sets).
When the arrays are remapped the contents of their shadow edges (see section 12) is not kept.
All elements of specified representation must be terminals of abstract machine tree (must not have descendants).
If PSRefPtr is NULL or *PSRefPtr is zero, then the subsystem, whose reference is in the map, will be used as the processor subsystem.
All processors of the system, specified by *PSRefPtr reference or by a reference, contained in the map, must belong to elementary intersection of the current processor system and the processor system, the parental processor system is mapped on.
The ranks of the abstract machine representation and the processor subsystem must be equal to corresponding ranks in map.
Remapped representation may be specified indirectly, if the header of the distributed array, created by function crtda_ with parameter *ReDistrParPtr is equal to1 or 3, is uses as parameter *AMViewRefPtr (see section 6).
The abstract machine representation, specified in the function call, can be not mapped earlier. In this case mredis_ function is executed as distr_ function, and *NewSignPtr parameter value is irrelevant.
The function returns non-zero, if remapped representation has a local part on the current processor, and zero in the other case.
long delmvm_(AMViewMapRef *AMViewMapRefPtr);
*AMViewMapRefPtr - reference to the map of the abstract machine representation.
The function deletes map of the abstract machine representation created by function amvmap_. After deleting map the reference may be used by the user program for its own goals.
The map can be deleted by delmvm_ function only if it was created in the current subtask and in the current program block (or its sub-block) (see sections 8 and 10).
To delete the map the function delobj_ can also be used (see section 17.5).
The function returns zero.
Note. One of possible usage of the abstract machine representation mapping functions according to the map is keeping and restoring the abstract machine mapping and therefore the allocation of the arrays, aligned with the mapping, in the procedures, dealing with external distributed arrays with their redistribution.
Note, that when map is used for mapping and remapping, the abstract machine representation, being the source of the map, may not exist.
5.7 Imbalanced block distribution
All notations, used in this section, except of newly introduced is assumed to be coincided with the notations from section 5.1.
Considered in section 5.1 the abstract machine representation mapping onto the processor system is the balanced distribution of the parental abstract machine resources onto the representation elements. In this case for k-th dimension of abstract machine representation the size of BLSIZEk block is assumed to be independent of a value of j-th coordinate of the processor system element. Such uniformity for each dimension is a result of supposed in section 5.1 equal weights of all its elements: the optimal weights of all processor coordinates are equal and equal to 1(see section 4.5).
Let us consider now a case of imbalanced elements of the processor system. Let the block BLSIZEk has a fixed size for k-th dimension (as in section 5.1), but a "number" of blocks per the processor system element with coordinate Pj for j-th dimension is equal to optimal weight of the coordinate. Then the first of the mapping rules, considered in section 5.1, (i.e. function Fj(I1, ... ,In)) is determined by inequalities
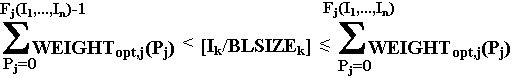
where WEIGHTopt,j(Pj) is optimal weight of the coordinate Pj.
The value BLSIZEk is determined as follows:
| BLSIZEk ={ | min(
DistrParamArray[j-1], AMSIZEk ) if DistrParamArray[j-1] ¹ 0 , [AMSIZEk / PSWEIGHTopt,j] if DistrParamArray[j-1] = 0 , |
where:
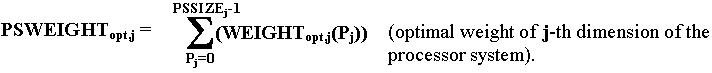
Since maximal allowed value Ik is
min( ([PSWEIGHTopt,j * BLSIZEk] - 1) , AMSIZEk - 1 ) ,
for full coverage of k-th dimension of the abstract machine representation by the mapping rule the following inequality must be satisfied:
AMSIZEk £ PSWEIGHTopt,j * BLSIZEk ,
It is achieved if
DistrParamArray[j-1] ³ AMSIZEk
/ PSWEIGHTopt,j
or if
DistrParamArray[j-1] = 0 .