5 Distribution of computations

5.1 Parallel loops

5.1.1 Parallel loop definition

The execution model of FDVM program and the programs in other data parallel languages too is SPMD (single program, multiple data). All the processors are loaded by the same program, but each processor according to owner-computes rule performs only those assignment statements that modify the variables located on the processor (own variables).

Thus computations are distributed in accordance with data mapping (data parallelism). In the case of a replicated variable, the assignment statement is performed at all the processors. In the case of the distributed array, the assignment statement is performed only at the processor (or processors) where the corresponding array element is located.

Identification of "own" statements and missing "others" can cause essential overhead when executing a program. Therefore the specification of computation distribution is allowed only for loops, satisfying the following requirements:

• the loop is of tightly nested loop with rectangular index space;
• distributed dimensions of arrays are indexed only by regular expressions of the form a*I + b , where I - is loop index;
• left sides of assignment statements of one loop iteration are allocated at the same processor and, therefore, the loop iteration is executed on the processor entirely.
• there is no data dependencies except reduction dependence and regular dependence along distributed dimensions;
• left side of assignment statement is a reference to distributed array, reduction variable or private variable (see section 5.1.3);
• there are no I/O statements and DVM directives inside parallel loop body.

A loop, satisfying these requirements, will be called parallel loop. An iteration variable of sequential loop, surrounding parallel loop or nested in the loop, can index the local (replicated) dimensions of the arrays only.

5.1.2 Distribution of loop iterations. PARALLEL directive

Parallel loop is specified by the following directive:

PARALLEL directive is placed before loop header and distributes loop iterations in accordance with array or template distribution. The directive semantics is similar to semantics of ALIGN directive, where index space of distributed array is replaced by loop index space. The order of loop indexes in list do-variable-list corresponds to the order of corresponding DO statements in tightly nested loop.

The syntax and semantics of directive clauses are described in the following sections:

Example 5.1. Distribution of loop iterations with regular computations.

	REAL  A(N,M), B(N,M+1), C(N,M), D(N,M)
CDVM$	ALIGN  (I,J)  WITH  B(I,J+1) :: A, C, D
CDVM$	DISTRIBUTE  B (BLOCK,BLOCK)
	.   .   .
CDVM$	PARALLEL  (I,J)  ON  B(I,J+1) 
	DO  10  I = 1, N
	DO  10  J = 1, M-1
	   A(I,J)   = D(I,J) + C(I,J)
	   B(I,J+1) = D(I,J) - C(I,J)
10	CONTINUE

The loop satisfies to all requirements of a parallel loop. In particular, left sides of assignment statements of one loop iteration A(I,J) and B(I,J+1) are allocated on the same processor through alignment of arrays A and B.

If left sides of assignment operators are located on the different processors (distributed iteration of the loop) then the loop must be split on several loops.

Example 5.2. Splitting the loop

The loop is split on 2 loops, and each of them satisfies to requirements of parallel loop.

5.1.3 Private variables. NEW clause

If a variable usage is localized in one loop iteration, then it must be specified in NEW clause:

The distributed arrays cannot be used as NEW-variables (private variables). The value of the private variable is undefined at the beginning of loop iteration and not used after loop iteration; therefore own copy of private variable can be used in each loop iteration.

Example 5.3. Specification of private variable.

CDVM$	PARALLEL  (I,J)  ON  A(I,J) , NEW ( X )
	DO  10  I = 1, N
	DO  10  J = 1, N
	   X = B(I,J) + C(I,J)
	   A(I,J) = X
10	CONTINUE

5.1.4 Reduction operations and variables. REDUCTION clause

Programs often contain loops with so called reduction operations: array elements are accumulated in some variable, minimum or maximum value of them is determined. Iterations of such loop may be distributed also, if to use the REDUCTION clause.

Distributed arrays may not be used as reduction variables. Reduction variables are calculated and used only inside the loop in statements of a certain type: the reduction statements.

Let us introduce some notation.

Reduction statement in the loop body is the statement of one of the following forms:

1)  rv = rv  op  er
     rv = er  op  rv

2)  rv = f( rv, er )
     rv = f( er, rv )

3)  if( rv  ol  er )   rv = er
   if( er  ol  rv )   rv = er

4)  if( rv  ol  er )  then 
       rv = er
       L( 1 ) = e1
         .  .  
       L( n ) = en
endif

     if( er  ol  rv )  then 
       rv = er
       L( 1 ) = e1
         .  .  
       L( n ) = en
endif

The correspondence between statement form, Fortran operation and FDVM reduction name is given below:

MAXLOC (MINLOC) operation assumes the calculation of maximal (minimal) value and defining its coordinates.

Example 5.4. Specification of reduction.

       S = 0
       X = 1.E10
       Y = -1.
       IMIN(1) = 0
CDVM$  PARALLEL ( I ) ON A( I ) ,
CDVM$* REDUCTION (SUM(S), MAX(X), MINLOC(Y,IMIN(1),1))

       DO  10  I = 1, N
	  S = S + A(I)
	  X = MAX(X, A(I))
	  IF(A(I) .LT. Y) THEN
	        Y = A(I)
		IMIN(1) = I
	  ENDIF
10     CONTINUE

5.2 Computations outside parallel loop

The computations outside parallel loop are performed according to own computation rule. Let statement

IF p THEN lh = rh

be outside parallel loop.

Here p – logical expression,

lh – left side of the assignment statement (a pointer to scalar or array element),
rh – right side of the assignment statement (expression).

Then the statement will be executed on the processor, where data with lh reference (own( lh ) processor) are allocated. All data in p and rh expressions must be allocated on the own( lh ) processor. If any data in p and rh expressions are not allocated on the own(lh) processor, they must be specified prior the statement in remote access directive (see section 6.1.2).

If lh is a reference to distributed array and data dependence between rh and lh exists, the it is necessary to replicate the distributed array by the directive

REDISTRIBUTE A( *,...,* ) or   REALIGN A( *,...,* )

before the statement execution.

Example 5.8. Own computations.

	PARAMETER  (N = 100)
	REAL  A(N,N+1),  X(N)
CDVM$	ALIGN  X( I )  WITH  A(I,N+1)
CDVM$	DISTRIBUTE  (BLOCK,*) :: A
	.   .   .
C	back substitution of Gauss algorithm
C	own computations outside the loops
C	
C	own computation statement
C	left and right sides are on the same processor
	X(N) = A(N,N+1) / A(N,N)
	DO  10  J = N-1, 1, -1
CDVM$	PARALLEL  ( I )  ON  A (I,*)
	DO  20  I = 1, J
	   A(I,N+1) = A(I,N+1) - A(I,J+1) * X(J+1)
20	CONTINUE
C	own computations in sequential loop,
C	nesting the parallel loop
	X(J) = A(J,N+1) / A(J,J)
10	CONTINUE

Note, that A(J,N+1) and A(J,J) are localized on the processor, where X(J) is allocated.

6 Remote data specification

6.1 Remote references definition

Data, allocated on one processor, and used on other one are called remote data. Actually, these data are common (shared) data for these processors. The references to such data are called remote references. Consider generalized statement:

IF (…A(inda)…) B(indb) = …C(indc)…

where

A, B, C - distributed arrays,
inda, indb, indc - index expressions.

In DVM model this statement will be executed on own(B(indb)) processor, that is on the processor, where B(indb) element is allocated. A(inda) and C(indc) references are not remote references, if corresponding elements of A and C arrays are allocated on own(B(indb)) processor. This is guarantied only if A(inda), B(indb) and C(indc) are aligned in the same point of alignment template. If the alignment is impossible or unrealizable, the references A(inda) and/or C(indc) should be specified as remote references. For multi-dimensional arrays this rule is applied to every distributed dimension.

By degree of processing efficiency remote references are subdivided on two types: SHADOW and REMOTE.

If B and C arrays are aligned and

inda = indc ± d ( d – positive integer constant),

then the remote reference C(indc) belongs to SHADOW type. Remote reference to multi-dimensional array belongs to SHADOW type, if distributed dimensions satisfy to SHADOW type definition.

Remote references, that don't belong to SHADOW type, are REMOTE type references.

Special set of remote references is set of references to reduction variables (see 5.2.4), that belongs to REDUCTION type. These references can be used in parallel loop only.

There are two kinds of specifications: synchronous and asynchronous for all types of remote references.

Synchronous specification defines group processing of all remote references for given statement or loop. During this processing, requiring communications, execution of the statement or the loop is suspended. Asynchronous specification allows overlapping computations and communications. It unites remote references of several statements and loops. To start reference processing operation and wait for its completion, special directives are used. Between these directives other computations, that don't contain references to specified variables, can be performed.

6.2 SHADOW type references

6.2.1 Specification of array with shadow edges

Remote reference of SHADOW type means, that remote data processing will be performed, using "shadow" edges. Shadow edge is a buffer, that is continuous prolongation of the array local section in the processor memory (see fig. 6.1). Consider following statement

A( i ) = B( i + d2) + B( i – d1)

where d1, d2 - integer positive constants. If both references to B array are remote references of SHADOW type, B array should be specified in SHADOW directive as B( d1 : d2 ), where d1 is low edge width, and d2 is high edge width. For multidimensional arrays the edges by each dimension should be specified. Maximal width for all remote references of SHADOW type is set in shadow edges specification.

SHADOW directive syntax.

Constraint.
The width of low shadow edge (low-width) and width of high shadow edge (high-width) must be integer non-negative constant expressions.

A specification of shadow edge width as width is equivalent to width : width specification.

The width of the both shadow edges of a distributed array is equal to 1 for each distributed dimension by default.

6.2.2 Synchronous specification of independent references of SHADOW type for single loop

Synchronous specification is a clause in PARALLEL directive.

Constraints:

• Width of the shadow edges filled by values must not exceed the maximal width specified initially in the SHADOW directive.
• If shadow edge widths is not specified, then the maximal widths are used.

Synchronous specification performing is renewing shadow edges by the values of remote variables before loop execution.

Example 6.1. Specification of SHADOW-references without corner elements

	REAL  A(100),  B(100)
CDVM$	ALIGN  B( I )  WITH  A( I )
CDVM$	DISTRIBUTE  (BLOCK) :: A
CDVM$	SHADOW  B( 1:2 )
	.   .   .
CDVM$	PARALLEL  ( I )  ON  A ( I ), SHADOW_RENEW ( B )
	DO  10  I = 2, 98
	   A(I) = (B(I-1) + B(I+1) + B(I+2) ) / 3
10	CONTINUE

When renewing shadow edges, the maximal widths 1:2 specified in SHADOW directive are used.

Distribution and shadow edge renewing scheme are shown on fig. 6.1.

Fig. 6.1. Distribution of array with shadow edges.

Two buffers, that are continuous prolongation of the array local section, are allocated on each processor. The width of low shadow edge is equal to 1 element (for B(I-1)), the width of high shadow edge is equal to 2 elements ( for B(I+1) and B(I+2)). If before loop entering to perform processor exchange according to scheme on fig. 6.1, the loop can be executed on each processor without replacing the references to the arrays by the references to the buffer.

Shadow edges for multidimensional distributed arrays can be specified for each dimension. A special case is when it is required to renew "a corner" of shadow edges. In such a case additional CORNER parameter is needed.

Example 6.2. Specification of SHADOW-references with corner elements

	REAL  A(100,100),  B(100,100)
CDVM$	ALIGN  B(I,J)  WITH  A(I,J)
CDVM$	DISTRIBUTE  A (BLOCK,BLOCK)
	.   .   .
CDVM$	PARALLEL  (I,J)  ON  A (I,J), SHADOW_RENEW (B(CORNER))
	DO  10  I = 2, 99
	DO  10  J = 2, 99
	   A(I,J) = (B(I,J+1) + B(I+1,J) + B(I+1,J+1) ) / 3
10	CONTINUE

The width of shadow edges of the array B is equal to 1 for both dimensions by default. As "corner" reference B(I+1,J+1) exists, the CORNER parameter is specified.

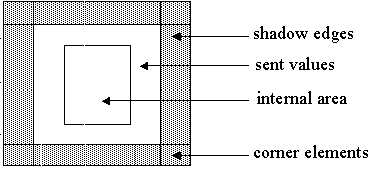
Fig. 6.2. Scheme of array local section with shadow edges.

6.2.3 Computing values in shadow edges. SHADOW_COMPUTE clause

In sections 6.2.1 and 6.2.2 the ways to renew values in shadow edges by data exchange between processors were described. At that new values of an array are calculated in one loop, but renewing is performed either before execution or during execution of other loop.

Under some conditions the values in shadow edges can be renewed without data exchange between processors. New values of shadow edges can be calculated in the same loop, where new values of the arrays are calculated. This way of shadow edge renewing is described by SHADOW_COMPUTE specification, which is clause of PARALLEL directive.

Let consider a parallel loop

CDVM$ PARALLEL (I1,I2,…,In) ON A(f1,f2,…,fk)

where A is identifier of the array, the loop iterations are distributed according to.

Let

{LH} - set of references to distributed arrays in left parts of the assignment statements of the loop body.
{RH} - set of references to distributed arrays in right parts (expressions) of the assignment statements of the loop body.

The following conditions must be satisfied to apply SHADOW_COMPUTE specification:

1. the width of shadow edges of distributed dimensions of arrays from {LH} and {RH} must be less than the width of shadow edges of corresponding dimensions of array A;
2. shadow edges of arrays from {RH} must be filled with the values, corresponding to values of the arrays.

During the loop execution the values of shadow edges of arrays from {LH} are renewed. The width of renewed part of every shadow edge is equal to the width of corresponding shadow edge of array A.

Example 6.3. SHADOW_COMPUTE specification.

CDVM$  DISTRIBUTE (BLOCK) :: A, B, C, D
CDVM$  SHADOW A(1:2)
CDVM$  SHADOW B(2:2)
CDVM$  PARALLEL ( I ) ON C( I ), SHADOW_COMPUTE,
CDVM$* SHADOW_RENEW( A, B )
       DO 10 I = 1, N
         C(I) = A(I) + B(I)
         D(I) = A(I) - B(I)
10     CONTINUE

As by default the width of shadow edges for C and D array is 1, the condition 1) is satisfied. Performing of SHADOW_RENEW specification satisfies the condition 2).

6.2.4 ACROSS specification of dependent references of SHADOW type for single loop

Consider the following loop

	DO  10  I = 2, N-1
	DO  10  J = 2, N-1
	   A(I,J) = (A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J)) / 4
10	CONTINUE

Data dependence exists between loop index i1 and i2 ( i1<i2 ), if both these iterations refer to the same array element by write-read or read-write scheme.

If iteration i1 writes a value and iteration i2 reads this value, then flow dependence, or simply dependence exists between the iterations.

If iteration i1 reads the "old" value and iteration i2 writes the "new" value, then anti-dependence i1¬  i2 exists between the iterations.

In both cases iteration i2 can be executed only after iteration i1.

The value i2 - i1 is called a range or length of dependence. If for any iteration i dependent iteration i + d (d is constant) exists, then the dependence is called regular one, or dependence with constant length.

The loop with regular computations, with regular dependencies on distributed arrays, can be distributed with PARALLEL directive, using ACROSS clause.

All the distributed arrays with regular data dependence are specified in ACROSS clause. The length of flow dependence (flow-dep-length) and the length of anti-dependence (anti-dep-length) are specified for each dimension of the array. There is no data dependence, if length is equal to zero.

Constraint:

• In each array reference, data dependence may appear only in one distributed dimension. For example, A(I-1,J), A(I,J+1) references are allowed, but A(I-1,J+1), A(I+1,J-1) references are forbidden.

If only the values of the sections of array are renewed in the loop but not whole array then these sections should be specified by SECTION clause.

Example 6.4. Specification of the loop with regular data dependence.

CDVM$	PARALLEL  (I,J)  ON  A(I,J), ACROSS (A(1:1,1:1))
	DO  10  I = 2, N-1
	DO  10  J = 2, N-1
	   A(I,J) = (A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J))/4
10	CONTINUE

Flow and anti- dependencies of length 1 exist for all dimensions of the array A.

ACROSS specification is implemented via shadow edges. The length of anti-dependence defines width of high edge renewing, and length of flow-dependence defines width of low edge renewing. High edges are renewed prior the loop execution (as for SHADOW_RENEW directive). Low edges are renewed during loop execution as remote data calculation proceeds. Actually, ACROSS-references are subset of SHADOW-references, that have data dependence.

Efficiency of parallel execution of ACROSS loop

An array dimension with data dependence will be called recurrent dimension.

Efficiency degree of ACROSS loop parallel execution depends on the number of distributed recurrent dimensions.

One-dimensional array. For one-dimensional distributed array with recurrent dimension only sequential execution is possible (see fig. 6.3).

Multi-dimensional array. For multi-dimensional array the following combinations of recurrent distributed dimensions can be selected according to degree of efficiency decreasing.

1) At least one non-recurrent dimension exists. The array and the loop are distributed along this dimension only. The loop is executed as usual parallel loop without ACROSS specification.

Example 6.5. Non-recurrent dimension parallelization.

CDVM$ DISTRIBUTE A( BLOCK, * )
CDVM$ PARALLEL ( I ) ON A( I, * )
      DO 30 I = 1,N1
      DO 30 J = 2,N2-1
30       A(I,J) = A(I,J-1) + A(I,J+1)

Note, that this way may be not most efficient, if N1 is much less then N2 and the number of processors (insufficient parallelism).

2) Only one recurrent dimension is distributed. Other dimensions are localized on every processor. Run-time system performs pipeline parallelization (see fig. 6.4). The size of pipeline step is defined on every computer automatically, depending on the loop execution time and the time of data passing when renewing shadow edges.

Example 6.6. Pipeline parallelization.

CDVM$ DISTRIBUTE A( BLOCK, * )
CDVM$ PARALLEL ( I, J ) ON A( I, J ), ACROSS( A( 1:1, 1:1 ))
      DO 40 I = 2,N1-1
      DO 40 J = 2,N2-1
40      A(I,J) = A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J)

Constraint of pipeline parallelization. For implementation of pipeline parallelization the following additional conditions must be satisfied:

• PARALLEL directive specifies two loop headers as minimum. One loop specifies distributed recurrent dimension, other loop specifies a local dimension of the array.
• If several arrays are specifying in ACROSS loop, these arrays should be aligned along recurrent distributed dimension and along the local dimension, indexed by the parallel loop.

3)  m>1 recurrent dimensions exist. The virtual processor arrangement contains m dimensions too. Run-time system automatically organizes parallel execution on hyper-planes of processor arrangement. Every hyper-plane has m-1 dimensions.

Example 6.7. Hyper-plane parallelization.

CDVM$ DISTRIBUTE A( BLOCK, BLOCK )
CDVM$ PARALLEL ( I, J ) ON A( I, J ) , ACROSS ( A( 1:1, 1:1 ))
      DO 50 I = 2,N1-1
      DO 50 J = 2,N2-1
50    A(I,J) = A(I,J-1) + A(I,J+1) + A(I-1,J) + A(I+1,J)

Two-dimensional arrangement of virtual processors is represented on fig. 6.5. The computations on processors, belonging to one hyper-plane (diagonal line), will be executed in parallel.

Fig. 6.3. Sequential execution

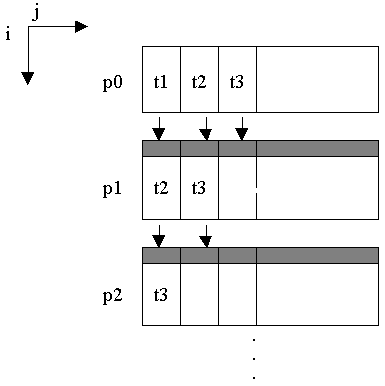
Fig. 6.4. Pipeline execution

Fig. 6.5. Parallelization by hyper-planes of virtual processor arrangement.

6.2.5 Asynchronous specification of independent references of SHADOW type

Updating values of shadow edges is indivisible (synchronous) exchange operation for unnamed group of distributed arrays. The operation can be divided into two operations:

• starting exchange;
• waiting for values.

While waiting for shadow edge values, other computations can be performed, in particular, computations on internal area of the local array section can be done.

The following directives describe asynchronous renewing of shadow edges for named group of distributed arrays.

Creation of a group.

Start of shadow edges renewing.

Waiting for shadow edges values.

SHADOW_START directive must be executed after SHADOW_GROUP one. After SHADOW_GROUP directive execution SHADOW_START and SHADOW_WAIT directives can be executed many times. Updated values of the shadow edges may be used only after SHADOW_WAIT directive execution.

A special case is using SHADOW_START and SHADOW_WAIT directives as shadow-renew-clause of parallel loop.

If the specification contains SHADOW_START, the surpassing computation of the values sent to the shadow edges is performed on each processor. Then the shadow edges are renewed and computation on internal area of the array local section is done (see fig. 6.2).

If the specification contains SHADOW_WAIT, the surpassing computation of the values in internal area of the local array section is performed. After completion of waiting for new values of shadow edges the calculations, using the values are performed.

Example 6.8. Overlapping computations and shadow edges updating.

	REAL  A(100,100), B(100,100), C(100,100), D(100,100)
CDVM$	ALIGN  (I,J)  WITH  C(I,J) :: A, B, D
CDVM$	DISTRIBUTE  (BLOCK,BLOCK) :: C
	.   .   .
CDVM$	SHADOW_GROUP  AB ( A, B )
	.   .   .
CDVM$	SHADOW_START  AB
	.   .   .
CDVM$	PARALLEL  (I,J)  ON  C(I,J),  SHADOW_WAIT  AB 
	DO  10  I = 2, 99
	DO  10  J = 2, 99
	   C(I,J) = (A(I-1,J) + A(I+1,J) + A(I,J-1) + A(I,J+1)) / 4
	   D(I,J) = (B(I-1,J) + B(I+1,J) + B(I,J-1) + B(I,J+1)) / 4
10	CONTINUE

The shadow edge width of distributed arrays is equal to 1 element for each dimension. Since SHADOW_WAIT directive is specified in parallel loop directive, the order of execution of the loop iterations is changed. At first computations on internal area of each local array section are performed. Then directive of waiting for updated values of shadow edges is performed. The loop execution is completed by computation of the values sent to shadow edges.

6.3 REMOTE type references

6.3.1 REMOTE_ACCESS directive

Remote references of REMOTE type are specified by REMOTE_ACCESS directive.

REMOTE_ACCESS directive can appear as a separate directive (its operating area is a following statement) or as a clause in PARALLEL directive (its operating area is parallel loop body).

If remote reference is specified as an array name without index list, all references to the array in a parallel loop (statement) are remote references of REMOTE type.

Let us consider remote reference to multi-dimensional array A( ind₁, ind₂,…,ind_k )
Let ind_j be index expression by j-th dimension.

Index expression is specified without changes in REMOTE_ACCESS directive, if

• j-th dimension is distributed dimension,
• ind_j = a * i + b, where a and b are not updated during loop execution (invariants).

In all other cases symbol “:” (total dimension) is specified instead of ind_j in REMOTE_ACCESS directive.

6.3.2 Synchronous specification of REMOTE type references

If in REMOTE_ACCESS directive a group name (remote-group-name) is not specified the directive is executed in synchronous mode. In boundaries of a statement or a parallel loop below the compiler replaces all remote references by references to a buffer. The values of remote data are passed prior the statement or the loop execution.

Example 6.9. Synchronous specification of REMOTE type references.

	DIMENSION  A(100,100), B(100,100)
CDVM$	DISTRIBUTE (*,BLOCK)  :: A
CDVM$	ALIGN  B(I,J)  WITH  A(I,J)
	.   .    .
CDVM$	REMOTE_ACCESS  ( A(50,50) )
C	replacing reference A(50,50) by reference to buffer
C	sending value A(50,50) to all the processors 
1	X = A(50,50)
	.   .   .
CDVM$	REMOTE_ACCESS  ( B(100,100) )
C	sending value B(100,100) to the buffer of processor own(A(1,1))
2	A(1,1) = B(100,100)
	.   .   .
CDVM$	PARALLEL  (I,J)  ON  A(I,J) ,  REMOTE_ACCESS  ( B(:,N) )
C	sending values B(:,N) to processors own(A(:,J))
3	DO 10  I = 1, 100
	DO 10  J = 1, 100
10	A(I,J) = B(I,J) + B(I,N)

First two REMOTE_ACCESS directives specify remote references for separate statements. REMOTE_ACCESS directive in parallel loop specifies remote data (matrix column) for all processors, array A is mapped on.

6.3.3 Asynchronous specification of REMOTE type references

If in REMOTE_ACCESS directive a group name (remote-group-name) is specified the directive is executed in asynchronous mode. To specify this mode following additional directives are required.

Group name definition.

The identifier, defined in the directive, can be used only in REMOTE_ACCESS, PREFETCH and RESET directives. The group remote-group is global object, its scope is the whole program.

Consider the following typical sequence of asynchronous specification of REMOTE type references:

CDVM$	REMOTE_GROUP RS
10	.   .   .
CDVM$	PREFETCH RS
	.   .   .
C	calculations, where remote references r1,…,rn don't take part
	.   .   .
CDVM$	PARALLEL .  .  .  , REMOTE_ACCESS (RS : r1)
	.   .   .
CDVM$	REMOTE_ACCESS  (RS : ri)
	.   .   .
CDVM$	PARALLEL .  .  .  , REMOTE_ACCESS (RS : rn)
	.   .   .
	IF( P ) GO TO 10

When given sequence of statements is executed first time, PREFETCH directive is not executed. REMOTE_ACCESS directives are executed in usual synchronous mode. At that the references are accumulated in variable RS. After execution of all the sequence of REMOTE_ACCESS directives the value of variable RS is union of subgroups of remote references r_i È ...È r_n.

When the sequence is executed the second and next time, PREFETCH directive performs surpassed sending of remote data for all the references, contained in variable RS. After PREFETCH directive and up to first REMOTE_ACCESS directive with the same group name other computations overlapping waiting for remote reference processing, can be performed. At that REMOTE_ACCESS directive doesn't cause any data sending.

Constraints:

• Repeated performance of PREFETCH directive is correct, only if the remote reference group characteristics (the loop parameters, array distributions and index expression values in remote references) are not updated;
• PREFETCH directive can be performed for the several loops (several REMOTE_ACCESS directives), if there are no data dependencies for distributed arrays specified in REMOTE_ACCESS directives.

If remote reference group characteristics were changed it is necessary to assign to the remote reference group undefined value using RESET directive. Then new accumulation of remote reference group will be done.

Consider the following fragment of multi-block problem. Simulation area is split on 3 blocks as is shown in fig. 6.6.

Fig. 6.6. Splitting simulation area.

Example 6.10. Using named group of regular remote references.

	REAL  A1(M,N1+1), A2(M1+1,N2+1), A3(M2+1,N2+1)
CDVM$	DISTRIBUTE  (BLOCK,BLOCK) :: A1, A2, A3
CDVM$	REMOTE_GROUP  RS
	DO  1  ITER = 1, MIT
	.   .   .
C	edge exchange along division line D
CDVM$	PREFETCH   RS 
	.   .   .
CDVM$	PARALLEL  ( I )  ON  A1(I,N1+1), REMOTE_ACCESS (RS: A2(I,2))
	DO  10  I = 1, M1
10	   A1(I,N1+1) = A2(I,2)
CDVM$	PARALLEL  ( I )  ON  A1(I,N1+1), REMOTE_ACCESS (RS: A3(I-M1,2))
	DO  20  I = M1+1, M
20	   A1(I,N1+1) = A3(I-M1,2)
CDVM$	PARALLEL  ( I )  ON  A2(I,1), REMOTE_ACCESS (RS: A1(I,N1))
	DO  30  I = 1, M1
30	   A2(I,1) = A1(I,N1)
CDVM$	PARALLEL  ( I )  ON  A3(I,1), REMOTE_ACCESS (RS: A1(I+M1,N1))
	DO  40  I = 1, M2
40	   A3(I,1) = A1(I+M1,N1)
	.   .   .
	IF (NOBLN)   THEN
C	redistribution of arrays to balance loading
	.   .   .
CDVM$	RESET  RS
	END IF
	.   .   .
1	CONTINUE

6.3.4 Asynchronous copying by REMOTE type references

If parallel loop contains only assignment statement without computations, the access by REMOTE type references can be performed more effectively using asynchronous copying of distributed arrays.

6.3.4.1 Loop and copy-statements

Consider following loop

      DO 10 I₁ = L₁,H₁,S₁
      . . .
      DO 10 I_n = L_n,H_n,S_n
10       A(f₁,…,f_k) = B (g₁,…,g_m)

where A, B - identifiers of different distributed arrays.

L_i, H_i, S_i – the loop invariants
f_i = a_i *I_i + b_i
g_j = c_j *I_j + d_j
a_i, b_i , c_j, d_j – integer expressions, the loop invariants (the expressions, which values are not updated during the loop execution).

Every loop variable I_l can be used at most in one expression f_i and at most in one expression g_j.

The loop can contain several statements satisfying the restrictions above. Such loop will be called copy-loop.

Copy-loop can be described by one or several copy-statements of the form

A(a ₁,…,a _k) = B(b ₁,…,b _m)

where
a _i = l_i : h_i : s_i
b _j = l_j : h_j : s_j
a _i, b _j are triplets of Fortran 90.

Copy-statement is similar to array section assignment statement in Fortran 90.

The rules of compact notation exist for triplets. Define these rules for triplet a _i for example.

1. If the whole dimension of array take part in coping, then
   a _i = :
2. If s_i = 1, then
   a _i = l_i : h_i
3. If L_i = h_i, then
   a _i = l_i

For copy-loop 10 triplet expressions are defined in the following way

Consider the following copy-loop

      REAL A(N1,N2,N3), B(N1,N3)
      DO 10 I1 = 1, N1
      DO 10 I2 = 2, N3-1
10       A(I1, 5, I2+1) = B(I1, I2-1)

Following copy-statement corresponds to this loop

A( :, 5, 3:N3 ) = B( :, 1:N3-2 )

6.3.4.2 Asynchronous coping directives

Asynchronous coping allows to overlap data passing between processors with execution of other statements.

Asynchronous coping is specified by combination of start coping directive (ASYNCHRONOUS ID) and the directive of waiting for coping completion (ASYNCWAIT ID). The correspondence of directives is defined by the same identifier ID.

6.3.4.2.1 ASYNCID directive

ASYNCID directive describes individual identifier for every pair of asynchronous copying directives.

The directive syntax:

6.3.4.2.2 F90 directive

F90 directive is prefix for every copy-statement.

Syntax.

6.3.4.2.3 ASYNCHRONOUS and END ASYNCHRONOUS directives

ASYNCHRONOUS and END ASYNCHRONOUS directives specify block construction.

Syntax.

All assignment statements in copy-loops should be described by F90 directives with corresponding copy-statement.

6.3.4.2.4 ASYNCWAIT directive

Syntax.

The example from section 6.3.4.1 can be specified as asynchronous coping in the following way.

CDVM$ ASYNCID TR
      REAL A(N1,N2,N3), B(N1,N3)
      . . .
CDVM$ ASYNCHRONOUS TR
CDVM$ F90 A( :, 5, 3:N3 ) = B( :, 1:N3-2 )
      DO 10 I1 = 1, N1
      DO 10 I2 = 2, N3-1
10       A(I1,5,I2+1) = B(I1,I2-1)
CDVM$ END ASYNCHRONOUS
      . . .
      sequence of statements,
      that are performed against a background of data passing
      . . .
CDVM$ ASYNCWAIT TR

6.4 REDUCTION type references

6.4.1 Synchronous specification of REDUCTION type references

If there is no group name in REDUCTION specification of parallel loop, it is synchronous specification and executed in the following way.

1. Local reduction calculation. During the loop execution on each processor local value of reduction is calculated for the part of data, allocated at the processor.
2. Global reduction calculation. After the loop completion inter-processor reduction of local values is automatically calculated. Resulted value is assigned to the reduction variable on each processor.

6.4.2 Asynchronous specification of REDUCTION type references

Asynchronous specification allows:

• to joint in one group the reduction variables, calculated in different loops;
• overlap global group reduction execution with other computations.

For asynchronous specification besides REDUCTION directive (with the group name) the following additional directives are required.

Typical sequence of asynchronous specifications of REDUCTION type is the following.

CDVM$	REDUCTION_GROUP  RD
	.   .   .
CDVM$	PARALLEL  .  .  .  , REDUCTION  (RD : d1)
C	local reduction d1
	.   .   .
CDVM$	PARALLEL  .  .  .  , REDUCTION  (RD : dn)
C	local reduction dn
	.   .   .
CDVM$	REDUCTION_START  RD
C	beginning of global reduction di È ...È dn
	.   .   .
CDVM$	REDUCTION_WAIT  RD
C	end of global reduction di È ...È dn

Constraints:

• Before executing REDUCTION_START directive, the reduction variables of the group may be used in reduction statements of parallel loops only.
• REDUCTION_START and REDUCTION_WAIT directives must be executed after the completion of the loop (loops) where the local values of the reduction variables were calculated. The only statements allowed between these directives are those that don't use the reduction variable values.
• REDUCTION_WAIT directive deletes the reduction group.

Example 6.11. Asynchronous specification of REDUCTION type references.

CDVM$	DISTRIBUTE  A (BLOCK)
CDVM$	ALIGN  B( I )  WITH  A( I )
CDVM$	REDUCTION_GROUP  RD 
	.   .   .
	S = 0
CDVM$	PARALLEL  ( I )  ON  A( I ), 
CDVM$*	REDUCTION (RD : SUM(S))
	DO  10  I = 1, N
10	   S = S + A(I)
           X = 0.
CDVM$	PARALLEL  ( I )  ON  B( I ), 
CDVM$*	REDUCTION (RD : MAX(X))
	DO  20  I = 1, N
20	   X = MAX(X, ABS(B(I)))
CDVM$	REDUCTION_START  RD
C	beginning of global reduction SUM(S) and MAX(X)

CDVM$	PARALLEL  ( I )  ON  A( I ) 
	DO  30  I = 1, N
30	   A(I) = A(I) + B(I)
CDVM$	REDUCTION_WAIT  RD
C	end of global reduction
 
	PRINT *, S, X

While the reduction group is executed the values of array A elements will be computed.