Fig. 1. DVM- model of data distribution on processors.
Predictor of DVM-program performance |
- last edited 27.12.00 -
Contents
1 Introduction
2 Predictor
implementation
2.1 Representation of the program as an hierarchy of intervals
2.2 Program execution characteristics on each processor
2.3 Main characteristics and their components
2.4 Source data for Predictor
3.1 General principles of simulation
3.2 Ordinary functions
3.3 Interval delimiter functions
3.4 Input/output functions
3.5 Create/delete object functions
3.6 Data and resources distribution functions
3.7 Functions of collective operation initialization
3.8 Functions of collective operation execution
3.9 Parallel loop functions
3.10 Unknown functions
4 Estimation of remote data access overhead
4.1 Main terms and definitions
4.2 Estimation of array redistribution exchanges
4.3 Estimation of distributed array edge exchanges
4.4 Estimation of reduction operation exchanges
4.5 Estimation of exchanges during remote array buffer loading
Appendix
1. Link from field name in output HTML-file to field name in
structure
_IntervalResult
Appendix
2. Definition of auxiliary functions and classes
Appendix
3. Main functions of time extrapolation
Appendix
4. Trace fragments and parameters of Lib-DVM functions simulated
by Predictor
References
The Predictor is intended for performance analysis and performance debugging of DVM-programs without usage of a real parallel computer (access to which is usually limited or complicated). With the Predictor user can get the predicted time characteristics of execution of his program on MPP or workstation cluster in more or less details.
The Predictor is the system for processing the trace information gathered by Run-Time library (Lib-DVM) during the program execution on a workstation and consists of two major components: trace interpreter (PRESAGE) and time extrapolator (RATER). The trace interpreter, using trace information and user-defined parameters, calculates and displays extrapolated time characteristics for the program execution on MPP or workstation cluster, calling functions of time extrapolator, which simulates parallel DVM-program execution. In fact, time extrapolator is a model of Lib-DVM library, low level message passing system (MPI), used by the library and hardware.
The performance of parallel programs on multiprocessor computers with distributed memory is determined by the following major factors:
The Predictor allows user to obtain the above and others characteristics and estimate quality of the parallel program.
There are three major stages of Predictor work:
2.1 Representation of the program as an hierarchy of intervals
For detailed program efficiency analysis user can split program into intervals and obtain performance characteristics for each interval.
The execution of the program can be represented as a sequence of alternating sequential or parallel intervals (groups of operators) execution. By default, the program is considered as one interval. Also user can define intervals by means of C-DVM and Fortran DVM languages. There is also opportunity to set a mode of compilation when the following loops can be declared as intervals
(Constraint: when Predictor is used, the integer expression with an interval must not appear inside parallel loop).
The user can also split any interval into smaller intervals or unite neighbor intervals (in order of execution) in new one, i.e. to present the program as hierarchy of intervals of several levels (the whole program is an interval of highest level 0).
The mechanism of splitting the program into intervals serves for more detailed analysis of behavior of the program during its execution. Looking through results with the help of the Predictor, user can set a depth of details i.e. ignore intervals of prescribed levels.
For simplification of the further description we shall enter the following notions. An interval will be called simple, if it does not contain other intervals (nested intervals). We refer to intervals including nested intervals as composite. Thus, the whole program is a interval tree: an interval of highest level (whole program) is a root of the tree; an interval of the lowest level is a leaf.
While processing trace information one of the intervals is an active interval (it is an interval of the lowest level containing program operator executed at the moment). For the active interval the following information is accumulated:
At this stage the number of communication operations within the interval is calculated:
In Predictor each interval corresponds with an object of “Interval” type which contains all necessary interval characteristics; during trace processing the interval tree builds. Each interval contains a vector of sub-objects of “Processor” type, each element of the vector saves characteristics of a processor involved in the interval execution. Thus after trace processing stage we have an interval tree with nodes of “Interval” type containing saved characteristics (IntervalType, EXE_count, source_file, source_line, num_op_io, num_op_reduct, num_op_shadow, num_op_remote, num_op_redist). At the same time characteristics of each involved processor are saved in the corresponding “Processor” object.
2.2 Program execution characteristics on each processor
“Processor” object contains the following characteristics of the processor involved in the interval execution:
As mentioned above accumulation of these characteristics is performed at the first stage of simulation – at the stage of trace processing; the characteristics are saved in “Processor” object for each interval and for each processor used for the interval execution.
While trace processing the tree of intervals (tree of “Interval” objects) is built, each interval contains a vector of “Processor” objects. The vector size is equal to the number of processors in the root processor topology, but processors involved in the interval execution are significant only.
2.3 Main characteristics and their components.
The possibility of processing the trace, accumulated by Lib-DVM at the stage of simulation execution of the program allows Predictor to give user the following main characteristics of the parallel program execution for the whole program as well as for each interval:
- Productive time (Productive_time), required for the parallel program execution on serial computer (consists of three parts):
- productive user program time (Productive_CPU_time) – time which the program spends for user calculations.
- productive system time (Productive_SYS_time) - time which the program spends for system calls (Lib-DVM calls).
- input/output time (IO_time) - time which the program spend for input/output.
- Total processor time (Total_time) calculated as a product of execution time by the number of processors.
Efficiency coefficient - is a ratio of the productive time to the total processor time.
For more detail information about above characteristics see [1].
After the tree of “Interval” objects is built the method “Integrate” is called for each object. This method calculate interval characteristics using corresponding characteristics of processor vector and characteristics of nested intervals. Finally HTML-file is created according to the interval tree: characteristics of every interval are written into the special “template” (see IntervalTemplate.cpp file). Correspondence between “Interval” object fields and HTML-file fields can be found in Appendix 1.
The following data serve for simulation: trace of the program execution on one processor, configuration information saved in some file (for example, “Predictor.par”) and command line options. To obtain necessary trace information the following parameters should be edited in the configuration file usr.par:
| Is_DVM_TRACE=1; | - trace on; |
| FileTrace=1; | - accumulate trace in files; |
| MaxIntervalLevel=3; | - maximum level of nested intervals; |
| PreUnderLine=0; | - do not underline “call” in trace file; |
| PostUnderLine=0; | - do not underline “ret” in trace file; |
| MaxTraceLevel=0; | - maximum trace depth for nested functions. |
Parameters PreUnderLine, PostUnderLine è MaxTraceLevel say to Lib-DVM that it is not necessary to accumulate lines of underscores in trace and it is not necessary to trace nested Lib-DVM calls, which gives much smaller size of the trace file.
Note. To run the parallel program on one
processor with explicitly defined processor configuration or with
dynamic set up for allocated processors it is necessary to define
corresponding “virtual” processor system by IsUserPS
and UserPS parameters.
For example, to define 2*2 “virtual” processor system
use the following parameter values:
| IsUserPS=1; | - use “virtual” processor system definition; |
| UserPS=2,2; | - “virtual” processor system topology. |
Let us consider the following trace fragment:
1. call_getlen_
TIME=0.000005 LINE=31 FILE=GAUSS_C.CDV
2. ArrayHandlePtr=951cd0;
…
3. ret_getlen_ TIME=0.000002
LINE=31 FILE=GAUSS_C.CDV
4. Res=4;
Line 1 identifies function of Lib-DVM (getlen_). It contains:
Line 2 (and probably lines after it) contains names and values
of actual function parameters. They are transformed into input
numerical values, packed in structures and used for simulation of
every Lib-DVM function.
Line 3 traces information about Lib-DVM function return. The only
value used by Predictor is the time (ret_time)
of the function execution (TIME=0.000002); it is usually summed
up in SYS_Time field of “Interval”
structure.
Line 4 contains function return value and used as it was
described for the line 2.
Every Lib-DVM function is processed by Predictor in accordance with its own algorithm, though many functions (“unknown” functions and “ordinary” functions) are processed by the same algorithm.
Predictor configuration information is defined in the special file (“Predictor.par”). The file contains the characteristics of the simulated multiprocessor system and has the following structure:
// System type = network | transputer
type = network;
// Communication characteristics (mks)
start time = 75;
send byte time = 0.2;
// Comparative processors performance
power = 1.00;
// Topology - optional
topology = {2, 2};
Lines beginning from “//” are comments. The parameter topology defines the virtual processor system topology, i.e. its rank and size on each dimension. The value network of type parameter means that the processor system is the network of workstations, and the value transputer means that the dedicated processor system uses transputer system as communication network. The linear approximation is used to calculate the time of transmission of n bytes:
T = (start time) + n *( send byte time),
where:
start time – start time of the data transmission;
send byte time - time of 1 byte transmission.
Parameter Power defines the ratio of the
productivity of the processor where Predictor is
working to the productivity of the processor where the parallel
program will be executed.
The order of parameters is arbitrary.
Structure of the output HTML-file is the same as the interval
structure in the program. Every HTML-file fragment corresponds to
some interval and contains data characterizing the interval, the
integral characteristics of the program execution on the interval
and also links to the fragments with the information about nested
intervals. HTML-file is a tree of intervals with special buttons
to traverse the tree in any direction.
3.1 General principles of simulation
At the first stage of simulation call-graph of Lib-DVM calls with actual parameters is built. Such a graph is a linear sequence of calls, as nested calls are not accumulated in the trace for Predictor. The call-graph is built in three steps:
Trace file ->
vector of TraceLine objects ->
vector of FuncCall objects.
At the second stage actual simulation of the program execution on the given multiprocessor system is performed.
To calculate the program execution characteristics Lib-DVM calls are simulated in the same order as they are in trace. During the simulation the following auxiliary structures and structure arrays are used:
During the call simulation array elements are created and deleted in the same order as they were during the program execution.
All support system functions can be divided in the following classes (from the point of view of simulation):
The principles of the simulation of the above functions will be considered in the next chapters.
In this group there are functions executed on every processor of simulated processor system (or its subsystem the current task is mapped on), and the time of their execution does not depend on configuration parameters and is equal to the time of execution on serial computer (taking into account performance of processors). If it is not specified explicitly, Lib-DVM function is simulated according to the following algorithm.
Simulation: times call_time and ret_time are added to Execution_time, time call_time is added to CPU_time, and ret_time is added to SYS_time of each processor. Besides, Insuff_parallelism_USR of each processor is added to the time calculated by formula:
T = Tcall_time * (Nproc - 1) / Nproc
and Insuff_parallelism_SYS is added to the time:
T = Tret_time * (Nproc - 1)/ Nproc
This is a base algorithm for time simulation. Further on we will suppose that execution time is simulated according to this algorithm, unless another algorithm is indicated explicitly.
3.3 Interval delimiter functions
In this group there are functions used as delimiters of intervals of the simulated program.
Functions:
| binter_ | Create user interval. |
| bploop_ | Create parallel interval. |
| bsloop_ | Create sequential interval. |
Simulation algorithm: according to the information from trace (source file name source_file, line number source_line, expression value (optionally) and interval type) an interval with same characteristics is found in the array of intervals nested in the current interval. Interval type depends on interval beginning function according to the following table:
| binter_ | User (USER) |
| bsloop_ | Sequential (SEQ) |
| bploop_ | Parallel (PAR) |
If interval is found its value of EXE_count increases by 1, otherwise a new element of the array of intervals nested in the current interval is created with EXE_count=1. The found interval or new interval becomes current.
Functions:
| einter_ | - end of user interval; |
| eloop_ | - end of parallel and sequential interval. |
Simulation algorithm: an interval which is external to the current interval becomes current. Times are corrected according to the base algorithm.
In this group there are functions used for data input/output. These functions are executed on input/output processor.
Simulation algorithm: time simulation algorithm differs from the base one. Function execution time is added to Execution_time and IO_time of input/output processor. Some of these functions broadcast execution result to all processors. In this case the broadcasting time is added to IO_comm of all processors.
3.5 Create/delete object functions
In this group there are functions used for creating and deleting different objects of Lib-DVM support system . When one of the functions is found in the trace it is necessary either to create and initialize or delete corresponding object in simulated multiprocessor system. As a rule creating and deleting objects are performed by corresponding constructor or destructor of the time extrapolator (RATER).
Function:
| crtps_ | - create subsystem of the given multiprocessor system. |
As subtask is run by:
long runam_ (AMRef *AMRefPtr)
where:
*AMRefPtr – reference to an abstract machine of the
subtask
and the current subtask is terminated by:
stopam_ ()
there is a stack of pairs (AM, PS) in from the Predictor (where runam_ push pair (AM, PS) in stack, and stopam_ pop stack). The top of the stack defines the current system statdefines root e: current ÀÌ and current PS. The bottom of the stack AM and PS (rootAM, rootPS).
Pair (AM, PS) is created by simulation of call:
mapam_ (AMRef *AMRefPtr, PSRef *PSRefPtr ).
Topology PS the corresponding AM is mapped on is read from Predictor configuration file (Predictor.par) during runam_ call. Predictor needs ÀÌ only once to establish the current PS. Characteristics and topology of source PS are found in the trace (from calls crtps_ and psview_ - AMRef and PSRef are needed).
Call getamr_ has a parameter:
IndexArray - array with i-th element containing index value of the corresponding element (i.e. abstract machine) along (i+1)-th dimension. The only thing which matters for Predictor is that a new AM is created and then mapped on new PS.
Simulation algorithm: on the base of information from parameter file an object of VM class is created (constructor VM::VM(long ARank, long* ASizeArray, int AMType, double ATStart, double ATByte)). Reference to this object and returned parameter PSRef are saved in the structure describing MPS.
Function:
| crtamv_ | - create representation of an abstract machine. |
Simulation algorithm: on the base of parameters from the trace (Rank and SizeArray[]) an object of AMView class is created (constructor AMView::AMView(long ARank, long* ASizeArray)). Reference to this object, actual parameter AMRef and return parameter AMViewRef are saved in a new element of array of abstract machine representations.
Function:
| crtda_ | - create distributed array. |
Simulation algorithm: on the base of parameters from the trace (Rank, SizeArray[] and TypeSize) an object of DArray class is created (constructor DArray::DArray(long ARank, long* ASizeArray, long ATypeSize)). Reference to this object and returned parameter ArrayHandlePtr are saved in a new element of array of distributed arrays.
Function:
| crtrg_ | - create reduction group. |
Simulation algorithm: an object of RedGroup class is created (constructor RedGroup::RedGroup(VM* AvmPtr)). Parameter AvmPtr is a reference to the object of VM class created while crtps_ function simulating. Reference to the created object and returned parameter RedGroupRef are saved in a new element of array of reduction groups.
Function:
| crtred_ | - create reduction variable. |
Simulation algorithm: an object of RedVar class is created (constructor RedVar::RedVar(long ARedElmSize, long ARedArrLength, long ALocElmSize)). Parameters ARedArrLength and ALocElmSize are actual function parameters, parameter ARedElmSize is calculated using RedArrayType parameter according to the following table:
| RedArrayType | C type | ARedElmSize |
| 1 (rt_INT) | int | sizeof(int) |
| 2 (rt_LONG) | long | sizeof(long) |
| 3 (rt_FLOAT) | float | sizeof(float) |
| 4 (rt_DOUBLE) | double | sizeof(doble) |
Reference to the created object and returned parameter RedRef are saved in a new element of array of reduction variables.
Function:
| crtshg_ | - create edge group. |
Simulation algorithm: an object of BoundGroup class is created (constructor BoundGroup::BoundGroup()). Reference to the created object and returned parameter ShadowGroupRef are saved in a new element of array of edge group.
Function:
| delamv_ | - delete an abstract machine representation. |
Simulation algorithm: an element with key AMViewHandlePtr is looked for in the array of abstract machine representations (AMViewRef). If it is found the object of AMView class is deleted (this object was created during crtamv_ function simulation) and then the element is deleted.
Function:
| delda_ | - delete distributed array. |
Simulation algorithm: an element with key ArrayHandlePtr is looked for in the array of distributed arrays. If it is found the object of DArray class is deleted (this object was created during crtda_ function simulation) and then the element is deleted.
Functions:
| delred_ | - delete reduction variable; |
| delrg_ | - delete reduction group. |
Simulation algorithm: an element with key RedRef (RedGroupRef) is looked for in the array of reduction variables (reduction groups). If it is found the object of RedVar (RedGroup) class is deleted (this object was created during simulation) and then the element is deleted.
Function:
| delshg_ | - delete edge group. |
Simulation algorithm: an element with key ShadowGroupRef is looked for in the array of edge group. If it is found the object of BoundGroup class is deleted (this object was created during simulation) and then the element is deleted.
3.6 Data and resources distribution functions
In this group there are functions used for initial distribution and redistribution of data and resources.
Function:
| distr_ | - | define mapping of an abstract machine representation on multiprocessor system (resource distribution). |
Simulation algorithm: an element with key AMViewRef is looked for in the array of abstract machine representations. If it is found the method AMView::DisAM(VM *AVM_Dis, long AParamCount, long* AAxisArray, long* ADistrParamArray) is called. Parameter AVM_Dis is a refference to the object of VM class created while crtps_ function simulating, other parameters are actual function parameters.
Function:
| align_ | - define location of distributed array (alignment). |
Simulation algorithm: an element with key ArrayHandlePtr is looked for in the array of distributed arrays. An element with key PatternRef is looked for either in the array of abstract machine representations or in the array of distributed arrays depending on the type of alignment template (AMView or DisArray). The method DArray::AlnDA(AMView*{DArray*} APattern, long* AAxisArray, long* ACoeffArray, long* AConstArray) is called for the object of Darray class which is from the first found record with key ArrayHandlePtr. The first parameter is reference to object of AMView or Darray type, depending on the type of alignment template corresponding to PatternRef key. Other parameters are actual function parameters. Besides, the type of alignment template is saved. Data transfer for distributed array alignment is ignored during the simulation.
Function:
| redis_ | - | redefine mapping of an abstract machine representation on multiprocessor system (resource distribution). |
Simulation algorithm: an element with key AMViewRef is looked for in the array of abstract machine representations. The method AMView::RDisAM(long AParamCount, long* AAxisArray, long* ADistrParamArray, long ANewSign) is called for the object of AMView class which is from the found record of the array of abstract machine representations. Other parameters are actual function parameters.
Time simulation algorithm differs from the base one. First, time counters of all processors are set to the same value which is equal to maximal counter values at the moment of the beginning of redis_ execution. The time which has been added into the counter sums with Execution_Time and with Synchronization of the given processor. The time returned by AMView::RDisAM(…) method is added to Execution_time and Redistribution of each processor.
Function:
| realn_ | - redefine location of distributed array. |
Simulation algorithm: an element with key ArrayHandlePtr is looked for in the array of distributed arrays. An element with key PatternRef is looked for either in the array of abstract machine representations or in the array of distributed arrays depending on the type of new alignment template (AMView or DisArray). The method DArray::RAlnDA(AMView*{DArray*} APattern, long* AAxisArray, long* ACoeffArray, long* AConstArray, long ANewSign) is called for the object of DArray class which is from the found record with key ArrayHandlePtr. The first parameter is reference to object of AMView or DArray type, depending on the type of template corresponding to PatternRef key. Other parameters are actual function parameters. The type of new alignment template is saved. If parameter NewSign is equal to 1, nested call of crtda_ function is looked for, and array key is substituted by the new value equal to return parameter ArrayHandlePtr of crtda_ function.
Time simulation algorithm differs from the base one. At first, time counters of all processors are set to the same value which is equal to maximal counter values at the moment of the beginning of realn_ execution. The time which has been added to the counter sums with Execution_Time and with Synchronization of the given processor. The time returned by DArray::RAlnDA(…) method is added to Execution_time and Redistribution of each processor.
3.7 Functions of collective operation initialization
In this group there are functions used for including reduction variable in reduction and including distributed array edge in edge group.
Function:
| insred_ | - include reduction variable in reduction group. |
Simulation algorithm: an element with key RedRef and corresponding object of RedVar class are looked for in the array of reduction variables; an element with key RedGroupRef and corresponding object of RedGroup class are looked for in the array of reduction groups. The method RedGroup::AddRV(RedVar* ARedVar) ) is called for the object of RedGroup class, the found object of RedVar class is a parameter.
Function:
| inssh_ | - include distributed array edge in edge group. |
Simulation algorithm: an element with key ShadowGroupRef and corresponding object of BoundGroup class are looked for in the array of edge groups; an element with key ArrayHandlePtr and corresponding object of DArray class are looked for in the array of distributed arrays. The method BoundGroup::AddBound(DArray* ADArray, long* ALeftBSizeArray, long* ARightBSizeArray, long ACornerSign) is called for the found object of BoundGroup class. The first parameter is refference to the found object of DArray class, parameter ALeftBSizeArray is an actual parameter LowShdWidthArray of inssh_ function, parameter ARightBSizeArray – actual parameter HiShdWidthArray, parameter ACornerSign – actual parameter FullShdSign.
3.8 Functions of collective operation execution
In this group there are functions used for collective operation execution.
Function:
| arrcpy_ | - copy distributed arrays. |
Simulation algorithm: elements with keys FromArrayHandlePtr and ToArrayHandlePtr are looked for in the array of distributed arrays. The function ArrayCopy(DArray* AFromArray, long* AFromInitIndexArray, long* AFromLastIndexArray, long* AFromStepArray, DArray* AToArray, long* AToInitIndexArray, long* AToLastIndexArray, long* AToStepArray, long ACopyRegim) is executed. Parameters are references to objects of DArray class from found records. Other parameters are actual parameters FromInitIndexArray[], FromLastIndexArray[], FromStepArray[], ToInitIndexArray[], ToLastIndexArray[], ToStepArray[], CopyRegim of arrcpy_ function.
Time simulation algorithm differs from the base one. At first, time counters of all processors are set to the same value which is equal to maximal counter values at the moment of the beginning of arrcpy_ execution. The time which has been added to the counter sums with Execution_Time and with Synchronization of the given processor. The time returned by ArrayCpy(…) function is added to Execution_time and Remote_access of each processor.
Function:
| strtrd_ | - start of reduction group. |
Simulation algorithm: an element with key RedGroupRef is looked for in the array of reduction group. The method RedGroup::StartR(DArray* APattern, long ALoopRank, long* AAxisArray) is called for the object of RedGroup class from the found element. Parameters APattern, ALoopRank and AAxisArray are from the structure which has been filled in during the last mappl_ call and corresponds to the parallel loop last mapped. An element with key RedGroupRef is created in the array of started reductions. The times of reduction beginning and reduction completion are saved in this element. The time of reduction beginning is equal to maximal value of processor counters at the moment of strtrd_ function call. The time of reduction completion is equal to sum of the time of reduction beginning and the time returned by RedGroup::StartR(…) method. If the pattern for mapping parallel loop is not distributed array but abstract machine representation an error is fixed and simulation is completed.
Time simulation algorithm differs from the base one. At first, time counters of all processors are set to the same value which is equal to maximal counter values at the moment of the beginning of strtrd_ execution. The time which has been added to the counter sums with Execution_Time and with Synchronization of the given processor.
Function:
| strtsh_ | - start of edge exchange of the given group. |
Simulation algorithm: : an element with key ShadowGroupRef is looked for in the array of edge group. The method BoundGroup::StartB() is called for the object of BoundGroup class from the found element. An element with key ShadowGroupRef is created in the array of started edge exchanges. The times of exchange beginning and exchange completion are saved in this element. The time of exchange beginning is equal to maximal value of processor counters at the moment of strtsh_ function call. The time of exchange completion is equal to the sum of the time of exchange beginning and the time returned by BoundGroup::StartB() method.
Time simulation algorithm differs from the base one. At first, time counters of all processors are set to the same value which is equal to maximal counter values at the moment of the beginning of strtsh_ execution. The time which has been added to the counter sums with Execution_Time and with Synchronization of the given processor.
Function:
| waitrd_ | - wait reduction completion. |
Simulation algorithm: an element with key RedGroupRef is looked for in the array of reductions already started. At the end of simulation this element is deleted.
Time simulation algorithm differs from the base one. For each processor the current value of time counter is compared with the time of reduction completion fixed during the simulation of strtrd_ function. The difference between above times is added to Reduction_overlap. If the value of processor time counter is less than the time of reduction completion, then the counter value is set to time of reduction completion. The time added to the counter sums to Execution_Time and Reduction_wait of the given processor.
Function:
| waitsh_ | - wait completion of edge exchange of the given group. |
Simulation algorithm: an element with key ShadowGroupRef is looked for in the array of edge exchanges already started. At the end of simulation this element is deleted.
Time simulation algorithm differs from the base one. For each processor the current value of time counter is compared with the time of exchange completion fixed during the simulation of strtsh_ function. The difference between above times is added to Shadow_overlap. If the value of processor time counter is less than the time of exchange completion, then the counter value is set as time of exchange completion. The time added to the counter sums to Execution_Time and Wait_shadow of the given processor.
In this group there are functions used for parallel loop initialization, distribution of its iterations between processors and the parallel loop execution.
Function:
| crtpl_ | - create parallel loop. |
Simulation algorithm: parameter Rank – parallel loop dimension is written in the structure describing parallel loop.
Function:
| mappl_ | - mapping parallel loop. |
Simulation algorithm: an object of ParLoop class is created (constructor ParLoop:: ParLoop (long ARank)). The method ParLoop::MapPL(AMView*{DArray*} APattern, long* AAxisArray, long* ACoeffArray, long* AconstArray, long* AInInitIndex, long* AInLastIndex, long* AInLoopStep) is simulated distribution of parallel loop iterations between processors. Then, for each processor, an object corresponding to the loop iteration block mapped on the given processor is created (constructor LoopBlock::LoopBlock(ParLoop *pl, long ProcLI)). Besides the key of the pattern map (PatternRef) and its type are saved in the structure describing the parallel loop.
Function:
| dopl_ | - define if it is necessary to continue parallel loop execution. |
Simulation algorithm: Time simulation algorithm differs from the base one. The total number of loop iterations (Niter) and the number of loop iterations on each processor (Ni) are calculated. The value Tfunc*(Ni/Niter) is calculated for each processor and added into Execution_time and CPU_time of the given processor. Besides, the domain of processor calculations is compared with calculation domains of other processors, the number of processors executing the same loop iterations is calculated (Nproc), for each processor executing the given part of the loop the following value is calculated
(Tfunc/Ni)*((Nproc-1)/Nproc)
and added to Insufficient_parallelism_Par.
Simulation algorithm: unknown functions are simulated according to the base algorithm. The warning about unknown function in the trace is output.
4 Estimation of remote data access overhead
4.1 Main terms and definitions
Before describing algorithms of estimation of remote data access overhead, let us consider the method of mapping calculations on distributed system. Diagram of array distributions on processor topology in DVM model is shown in Fig. 1.
Fig. 1. DVM- model of data distribution on processors.
Let us introduce a notion of Abstract machine representation (for short – Template or AMView) – a special array intended for providing two-stage arrays mapping and calculations mapping on processor system: first they (Darrays) are mapped on AMView, which then are mapped on processor system (VM). The first mapping is entirely determined by interrelation between data and calculations characteristic for algorithm and do not depend on architecture or configuration of distributed computational system. The second mapping serves for the parallel program tuning according to available system resources.
While aligning (realigning) a distributed array, an ordinary distributed array that has already been mapped on some AMView can act as AMView itself.
Information about aligning arrays on template can be received using DArray::AlnDA function call. Distribution of the template on the processor system is performed using AMView::DisAm.
4.2 Estimation of array redistribution exchanges
Let’s consider the algorithm of computing overhead charges of realigning the array over template (realign). This algorithm is implemented in Darray:RalnDA function, which returns amount of time spent in exchanges between processors during the given operation. Besides, the function changes the information of the given array, about the template it is mapped on and by which rule, according to function parameters. Correction of lists of aligned arrays is performed, for corresponding templates.
At the first stage of algorithm we check the value of the ANewSign input parameter. If the value is non-zero, contents of the realigned array will be updated, therefore it is not necessary to transfer useless elements, so function returns zero. Otherwise, algorithm continues working.
Saving the information about the array position before realigning, we get the information about it’s new position using DArray:AlnDA function.
Then, using CommCost::Update(DArray *, DArray *), array CommCost::transfer (filled with zeros at first) is changed, according to the information about array position obtained before. This array (CommCost::transfer) contains the information about number of bytes being transferred between every two processors.
And finally, the amount of time is computed based on data in transfer array, using function CommCost::GetCost.
Algorithm implemented in Update function:
For finding the time spared by processors, in GetCost function, one of the two algorithms is used. The choice of algorithm depends on distributed processor system type. In case of the net with bus organization, the sought time is computed by this formula:
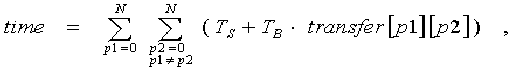
where N is number of the processors, Ts – start time of the exchange operation, TB – time to send one byte. This formula is a consequence of the fact that several messages can’t be simultaneously sent over the net and, consequently, total time equals to the sum of all exchange times between any two non-coinciding processors.
Total time for the transputer grid generally depends on the shortest way between the two processors most distant from each other, if exchanges between them exist. Also, while evaluating this time it is necessary to consider the possibility of message pipelining. As follows from this remarks, we can make up an algorithm and a formula to determine overhead charges:
![]()
If l > 1, pipelining of the message is possible. So, at first we examine the following function for extremes, which describes the dependence of LB from S – size of the message sent during one pipeline phase:
We get that minimum is reached when:
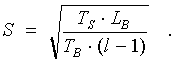
Considering that the message size and the number of phases are integers, we come to this expression:
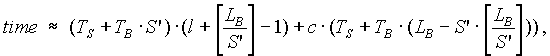
where S’ = [S] (S’ = 1, if [S] = 0); c Î {0, 1} – an evidence that S’ doesn’t divide LB. In order to find the exact value we find the time by the same formula, but in the integer points near to S’. If they are bigger, value in the point S’ is the sought value. Otherwise we perform the decreasing search, until value on the stage k is bigger than value on k-1. Then, the sought time is the value on stage k-1. Algorithm stops.
As a conclusion, we’ll consider the algorithm of finding overhead charges while redistributing the template. These charges arise because all the distributed arrays aligned by the template using DArray::AlnDA (both directly and indirectly), will be mapped on the template again, after it changes it’s position in the processor system. Consequently, they will change their position, and it will lead to the exchanges. The given algorithm is implemented in AMView::RdisAM, which returns the time spent in the interprocessor exchanges while performing this operation. Also, the function replaces the information for the given template, about the rule by which it was mapped on the processor system (received by the AMView::DisAM function), with information about it’s new position according to the new parameters, given in the function call.
In the first stage of the algorithm we check the value of the ANewSign input parameter. If the value is non-zero, contents of all the distributed arrays aligned with the given template will be updated, therefore it is not necessary to transfer useless elements, so function returns zero. Otherwise, algorithm continues working.
Saving the information about the template position before redistribution, we get the information about it’s new position after the given operation using the AMView::DisAM function. It is necessary in order to know how the arrays aligned by this template are positioned before and after the redistribution.
Then, for every array aligned by the given template, array CommCost::transfer (filled with zeros at first) is changed, using CommCost::Update(DArray *, DArray *), according to the information about the array position before and after the redistribution received before.
And finally, the sought amount of time is computed based on data in the transfer array, using the function CommCost::GetCost.
4.3 Estimation of distributed array edge exchanges
Let’s consider the algorithm of computing the time needed for the exchange of the given group bounds. It consists of two parts.
Algorithm implemented in CommCost::GetCost was described in the previous paragraph, so we’ll consider algorithm of the BoundGroup::AddBound function:
4.4 Estimation of reduction operation exchanges
The algorithm of determining time spent in exchanges during the reduction operations is implemented in the RedGroup::StartR function. Before the description of algorithm, we’ll show what preparatory work is performed.
When another reduction variable is added to the reduction group, counter of the number of sent bytes (TotalSize) is increased by the size of the reduction variable and auxiliary information (given for some of the reduction operations) in bytes using the RedGroup:AddRV function. Information about the reduction variable type isn’t taken into consideration when evaluating the exchange time.
Description of StartR function:
time = (TS + TB TotalSize) × (Ni1 × ... × Nik + N – 2) ,
where exchange operation, TB – time to send one byte, Nik – N is the number of processors, Ts – start time of the number of the processors by the processor system dimension with number loopAlign[ik], on which the loop iterations are present. Function returns the value calculated.
time = (TS + TB × TotalSize) × (2 × Distance + ConerDistance),
where ConerDistance is distance from the given sections to the most distant corner processor. Return the resulting value.
4.5 Estimation of exchanges during remote array buffer loading
If aligning the arrays doesn’t get us rid of the remote data and no shadow edges can be used to access them, their bufferization is performed through the separate buffer array on every processor. Estimated time spent during the buffer loading is calculated in the ArrayCopy function. The interface of this function allows further expansion of the output language, therefore some parameters aren’t used at this stage. Exactly, exchanges during the replication of the distributed array (array that is read) over all the processors in the processor system are evaluated in this function. Below there is a description of algorithm implemented in ArrayCopy function:
In the CopyUpdate function, the following actions are performed:
Appendix 1. Link from field name in output HTML-file to field name in structure _IntervalResult ==>