No Title

Домашнее задание 3.
Срок сдачи: 06/03/2000.

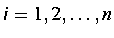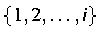1.: Предложите алгоритм динамического программирования для решения задачи о планировании работ, основанный на последовательном вычислении m_i для $i=1,2,\ldots,n$ , где m_i является размером наибольшего подмножества совместных работ из множества $\{1,2,\ldots,i\}$ . Входные данные отсортированы в порядке возрастания времен окончания работ. 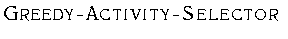Сравните время работы вашего алгоритма со временем работы $\ensuremath{\textsc{Greedy-Activity-Selector}}$ .
2.: Дано множество занятий, которое нужно распределить по большому количеству аудиторий. Каждое занятие проходит в интервале времени [s_i, f_i) (как и в задаче, рассмотренной на лекции). Необходимо для каждого занятия назначить аудиторию таким образом, чтобы было использовано минимальное количество аудиторий. Предложите <<жадный>> алгоритм и обоснуйте его корректность.
3.: В задаче о планировании работ, рассмотренной на лекции, не всякая <<жадная>> стратегия дает множество взаимно совместных работ максимальной мощности. Приведите пример, что стратегия, основанная на выборе работы наименьшей продолжительности, совместимой с уже выбранными работами, не работает. Приведите пример, что стратегия, основанная на выборе работы, накладывающейся на наименьшее количество оставшихся работ, не работает.
4.: Докажите, что дробная задача о рюкзаке имеет свойство <<жадного>> выбора.
5.: Предложите эффективный алгоритм, который для множества точек 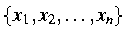$\{x_1,x_2,\ldots,x_n\}$ на вещественной прямой определит минимальное количество закрытых интервалов единичной длины, которые содержат все данные точки. Обоснуйте корректность алгоритма.

Alexander Chernov
2000-02-28