Домашнее задание 1.
Срок сдачи: 21/02/2000.

1.
Покажите, что $an+b=\Theta(n)$.

2.
Каково математическое ожидание числа выполнений строки 4 алгоритма \ensuremath{\textsc{Minimum}} в предположении, что все перестановки входной последовательности равновероятны. Докажите, что математическое ожидание равно $\Theta(\lg n)$.

3.
Быстрая сортировка. 
     Quicksort(A,p,r)
[1]    if p < r then
[2]      q := Partition(A,p,r)
[3]      Quicksort(A,p,q)
[4]      Quicksort(A,q+1,r)
[5]    end

Покажите, что среднее время работы алгоритма равно $\Theta(n\lg n)$.

Указания. Найдите рекуррентное соотношение, описывающее T(n). Предположите, что $T(n) \leqslant a n \lg n + b$, и докажите утверждение по индукции, используя следующее неравенство:

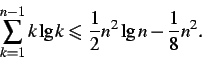
\begin{displaymath}\sum_{k=1}^{n-1}k \lg k \leqslant\frac{1}{2}n^2\lg n - \frac{1}{8}n^2. \end{displaymath}

4.
Алгоритм сортировки называется стабильным, если порядок равных элементов в отсортированной последовательности сохраняется. То есть, если в исходной последовательности ai = ajпри i < j, то в отсортированной последовательности $\pi(i) < \pi(j)$, где $\pi(k)$ -- позиция, на которой оказывается элемент, находившийся в исходной последовательности на позиции k.

Является ли алгоритм \ensuremath{\textsc{Quicksort}} стабильным? Как он должен быть модифицирован для достижения стабильности?

5.
Напишите нерекурсивную версию алгоритма \ensuremath{\textsc{Quickselect}}.

6.
Даны два отсортированных массива A[1..n] и B[1..n] по n элементов, не содержащие одинаковых элементов. Опишите алгоритм, находящий медиану 2n элементов за время $O(\lg n)$.


Alexander Chernov
2000-02-14